现代数字逻辑电子技术概论
二十一世纪,数字化浪潮席卷了电子工业领域,与传统的模拟电子系统相比,数字系统具备更加优异的精确与可靠性,逐步取代了许多模拟电路的应用场景。数字逻辑电路是对数字信号进行算术与逻辑运算的电路,以逻辑门作为基本电路单元(最早采用 TTL 工艺,伴随半导体工艺技术的不断进步,目前已经逐步被 CMOS 工艺取代),数字电路可以分为组合逻辑电路(基本逻辑门)和时序逻辑电路(逻辑门 + 反馈逻辑回路)两大类。

本篇文章讲解了数字逻辑电路的分析与设计所涉及到的基础理论,首先讲解了数制、码制和逻辑代数等基础知识,接着重点描述组合逻辑电路和时序逻辑电路的分析与设计方法,然后讨论了各种数字集成电路(
含门电路、可编程逻辑元件、半导体存储器)的原理以及使用方法,并且介绍了硬件描述语言与可编程逻辑器件的相关知识,最后一部分讲解AD/DA转换以及脉冲波形的产生和转换电路。
数字逻辑概论
数字信号
模拟信号的电压或者电流在幅值和时间上都是离散的:
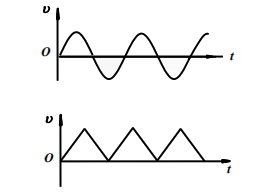
数字信号的电压或者电流的幅值随着时间连续变化:
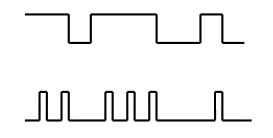
数字信号可以采用高、低电平来表示,它们统称为逻辑电平:
- 低电平:电压值位于 \(0
\sim V_{L(max)}\) 范围内,通常表示逻辑
0; - 高电平:电压值位于 \(V_{H(min)} \sim +V_{DD}\)
范围内,通常表示逻辑
1; - 电压值位于 \(V_{L(max)} \sim V_{H(min)}\) 范围内没有定义,不能使用;
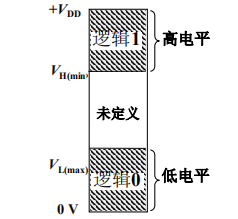
CMOS 元器件电压值范围与数字逻辑电平之间的对应关系:
| 电压范围 | 逻辑值 | 逻辑电平 |
|---|---|---|
| \(3.5V \sim 5V\) | 1 |
高电平 H |
| \(0V \sim 1.5V\) | 0 |
低电平 L |
| \(1.5V \sim 3.5V\) | 无定义 | 无定义 |
数字波形是信号的逻辑电平相对于时间的图形化表达方式:
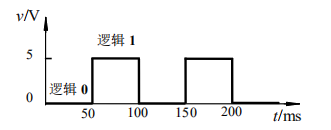
实际脉冲波形在高、低电平跳变时,边沿不是陡直的,都需要经历一个过渡过程:
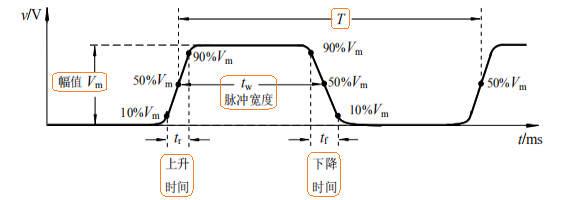
- 脉冲幅值 \(V_m\):脉冲电压的最大变化幅度,即图中高电平的电压值,单位为伏特
V; - 上升时间 \(t_r\):指矩形脉冲上升沿从 \(10\% V_m\) 上升到 \(90\% V_m\) 时所经历的时间,单位为纳秒
ns; - 下降时间 \(t_f\):指矩形脉冲下降沿从 \(90\% V_m\) 下降到 \(10\% V_m\) 时所经历的时间,单位为纳秒
ns; - 周期 \(T\):周期性重复的矩形脉冲中,两个相邻脉冲之间的时间间隔。有时也用频率来表示,即 \(f = \frac{1}{T}\);
- 脉冲宽度 \(t_w\):从矩形脉冲上升沿的中间点 \(50\% V_m\) 开始,到脉冲下降沿的中间点 \(50\% V_m\) 为止的一段时间;
- 占空比 \(q\):表示矩形脉冲宽度(高电平)占据整个周期的百分比;
▶【例题】假设周期性矩形脉冲波形的高电平持续时间为
6ms,低电平的持续时间为 10ms,求解占空比
q 和频率 f ?
▶【解答】根据条件可以得到脉动宽度 \(t_w = 6ms\) 和周期 \(T = 6ms + 10ms = 16ms\),从而可以计算出:
\[ \begin{aligned} 占空比 &\implies q = \frac{6 ms}{10 ms} \times 100\% = 37.5\% \\ 频率 &\implies f = \frac{1}{T} = \frac{1}{16 \times 10^{-3}s} = 62.5 Hz \end{aligned} \]
数制
数制是一种计数规则,主要是指每一位的构成,以及从低位向高位的进位。例如:十进制是以
10 为基数的计数体制,采用
0、1、2、3、4、5、6、7、8、9
十个数值,其进位的规则是逢十进一。

二进制则是以 2 为基数,采用
0 和 1
两个数值,其进位规则是逢二进一,其中左侧是最高有效位(MSB),右侧为最低有效位(LSB)。
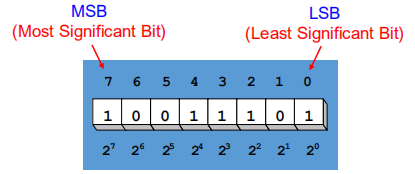
注意:二进制数中的每 1 个二进制数称为
1 bit位,而 8 位二进制数被称为1 Byte字节。
下面的表格对照了 十(Decimal)、二(Binary)、八(Octonary)、十六(Hexadecimal)进制的特点:
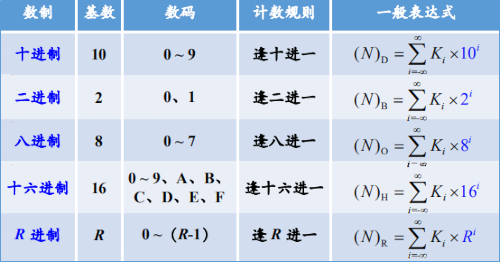
下面的表格展示了常用进制数值的换算关系:
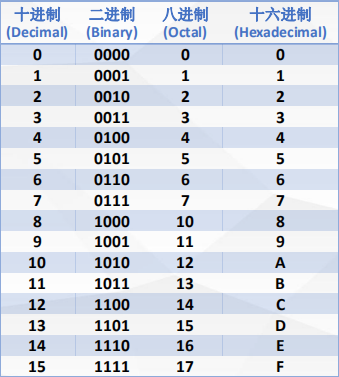
二进制 ➔ 十进制
二进制数转换为十进制的方法,按照按权展开公式进行计算。即将每个位上的数值与相应位置的权相乘,最后再求和。
▶【例题】将二进制整数 \((1001 1101)_2\) 转换为十进制数。
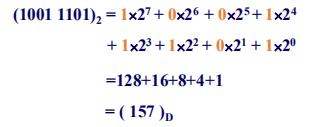
▶【例题】将二进制小数 \((0.1011)_2\) 转换为十进制数。
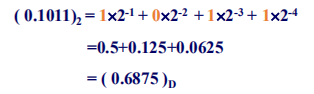
十进制整数 ➔ 二进制
十进制整数转换为二进制数主要有加权求和法、除二取余法两种方式。
加权求和法
加权求和法是通过确定一组二进制权,让它们的和等于已知十进制数。
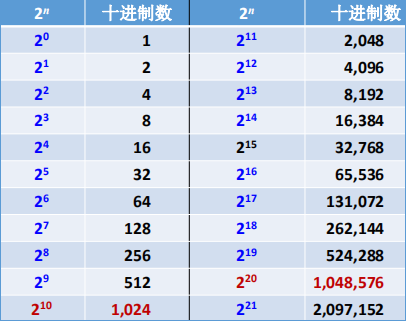
▶【例题】将十进制整数 \((9)_{10}\) 转换为二进制数。
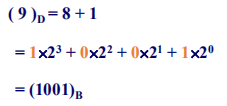
▶【例题】将十进制整数 \((82)_{10}\) 转换为二进制数。
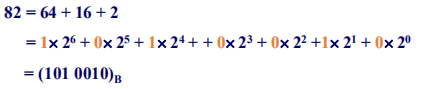
▶【例题】将十进制整数 \((125)_{10}\) 转换为二进制数。
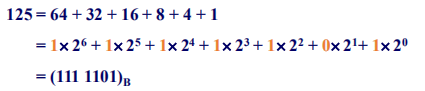
除二取余法
除二取余法是将十进制整数除以 2
取其余数,所得之商再除以 2,再取其余数,如此重复直到商为
0,每次得到的余数就构成了二进制数的对应位。其中,第一个余数为二进制数的最低位,最后一个余数为二进制数的最高位。
▶【例题】将十进制数 \((45)_{10}\) 转换为二进制数。
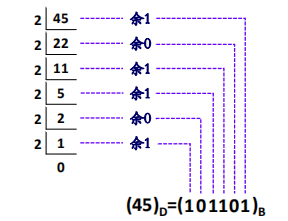
十进制小数 ➔ 二进制
十进制小数转换为二进制数同样可以选择加权求和法、除二取余法两种方式。
加权求和法
加权求和法是通过确定一组二进制权,让它们的和等于已知十进制数。
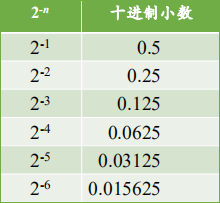
▶【例题】将十进制小数 \((0.625)_{10}\) 转换为二进制数。
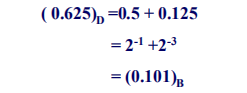
除二取余法
除二取余法是将十进制整数除以 2
取其余数,所得之商再除以
2,再取其余数,如此重复直至小数部分为 0
或者小数部分的位数满足误差要求,然后四舍五入为止,每次得到的整数就构成了二进制数的对应位。
▶【例题】将十进制小数 \((0.3125)_{10}\) 转换为二进制数。

▶【例题】将十进制小数 \((0.562)_{10}\) 转换为二进制数,要求转换误差小于 \(1\%\)。
如果误差要求小于 \(1\%\),那么 \(2^{-m} \le 1\% \implies m \ge \frac{2}{\lg 2} = 6.64 \implies m = 7\),即保留 7 位二进制结果即可:

接下来校对上面得到二进制结果 \((0.1000111)_{2}\) 的转换误差,
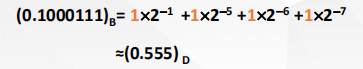
由于 \((0.562)_{10} - (0.555)_{10} \approx 0.7\%\) 误差小于 \(1\%\),所以最后得到的二进制结果满足转换误差的要求。
二进制 ➔ 十六进制
由于 4 位二进制数恰好拥有 16 个状态,如果将这 4
位二进制数看作整体,其进位输出正好是逢十六进一,所以可以采用分组转换法,即以二进制数的小数点为基准,整数部分从右至左每
4 位分成一组,而小数部分从左至右每 4 位也分成一组,不足 4 位的以
0 进行补足,然后将每一组数以一个十六进制数代替。
▶【例题】将二进制小数 \((1101\ 1001\ 1011\ 0011 . 01)_{2}\) 转换为十六进制数。

所以,最终的转换结果为 \((1101\ 1001\ 1011\ 0011.01)_2 = (D9B3.4)_{16}\)。
十六进制 ➔ 二进制
将每个十六进制数改写为等值的 4 位二进制数即可,并且保持高低位的次序不变。
▶【例题】将十六进制小数 \((4E6.97C)_{16}\) 转换为二进制数。

所以,最终的转换结果为 \((4E6.97C)_{16} = (0100\ 1110\ 0110. 1001\ 0111\ 1100)_2\)。
十六进制 ➔ 十进制
可以根据按权展开公式进行计算,即将每个数与相应位置上的权相乘,然后再进行求和运算。
▶【例题】将十六进制小数 \((3A.C)_{16}\) 转换为十进制数。
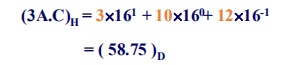
所以,最终的转换结果为 \((3A.C)_{16} = (58.75)_{10}\)。
十进制 ➔ 十六进制
将十进制转换为十六进制,可以先转换为二进制数,然后再将得到的二进制数转换为等值的十六进制数。
当然,也可以采用除以十六取余法直接从十进制整数转换为十六进制。
▶【例题】将十进制整数 \((650)_{10}\) 转换为十六进制数。
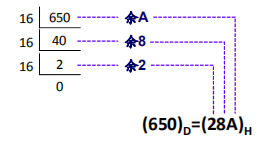
对于十进制小数转换为十六进制,则需要使用乘以十二取整法。
▶【例题】将十进制小数 \((0.75)_{10}\) 转换为十六进制数。

二进制算术运算
当两个二进制数表示两个数量大小时,它们之间可以进行数值运算,这种运算称为算术运算。
加法
二进制数加法的运算规则与十进制数加法类似,只是其进位规则为逢二进一。
对于一位二进制数的相加运算,会向左侧相邻的高位产生进位:
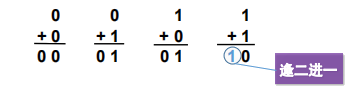
对于多位二进制数的加法从最低位(最右侧)开始,每次取被加数和加数的一位相加,然后逐一向左侧相邻的高位进位。
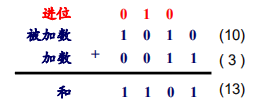
减法
二进制减法运算当中,当 0 减去 1
不够减时,需要向左边高位进行借位,借的这一位作为 10
处理(即十进制数 2),也称为借一为二。
\[ \begin{aligned} 0 - 0 &= \color{Red}0 &\implies 借位为\ \color{Green}0 \\ 1 - 0 &= \color{Red}1 &\implies 借位为\ \color{Green}0 \\ 1 - 1 &= \color{Red}0 &\implies 借位为\ \color{Green}0 \\ 0 - 1 &= \color{Red}-11 &\implies 借位为\ \color{Green}1 \\ \end{aligned} \]
当两个一位二进制数相减时,如果低位向本位的借位一直为
1,那么计算的四种情况为:
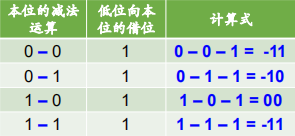
当两个多位二进制数相减时,从最低位(最右边)开始,每次取被减数与减数的
1
位相减;同时还要考虑低位向本位的借位,如果被减数小于减数,就要将减数与被减数交换位置,用减数减去被减数,然后在差值的前面添加负号-。
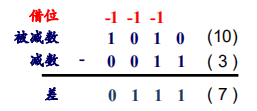
乘法
被乘数与乘数中某一位相乘的结果,称为部分积。
\[ \begin{aligned} 0 \times 0 &= \color{Red}0 \\ 0 \times 1 &= \color{Red}0 \\ 1 \times 0 &= \color{Red}0 \\ 1 \times 1 &= \color{Red}1 \\ \end{aligned} \]
▶【例题】计算两个四位二进制数 \(1011\) 和 \(1001\) 的积?
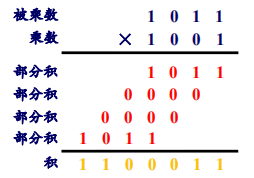
所以,多位二进制数 \(1011\) 乘以 \(1001\) 的积为 \(1100011\)。
注意:计算机当中,乘法运算是通过左移被乘数、加法两种运算共同完成的。
除法
从被除数的最高位开始,逐位向低位不断减去除数,够减时商为
1,不够减时商为
0,这样不断减下去就可以求得商。在二进制除法当中,每一位商的值为
0 或者 1。
\[ \begin{aligned} 0 \div 1 &= \color{Red}0 \\ 1 \div 1 &= \color{Red}1 \\ \end{aligned} \]
注意:类似于十进制的除法,二进制的除数不能为
0,否则没有意义。
▶【例题】计算两个四位二进制数 \(1010\) 和 \(111\) 的商?

注意:计算机当中,除法运算是通过右移被除数、减法两种运算共同完成的。
有符号数
日常生活当中,通常在一个数的前面采用 + 号表示正数,减号
- 表示负数。由于数字系统只能识别和处理 0 和
1 表示的二进制数据,因此通常将正号 +
用 0表示负号用 1
表示。将数的符号和值分别用 0 和 1
进行编码,所表示出来的二进制数称为机器数,机器数真正的值(即用正负符号表示的十进制或二进制数值)称为真值。机器数可以分为有符号和无符号两种类型:
- 无符号数:所有二进制位全部用来表示数值,例如 8
位无符号整数的 8 位全部都是用来表示数值的数值位:

- 有符号数:符号和数值分别采用二进制数进行表示,例如
8
位无符号整数左边的最高位作为符号位,其余位为数值位:

有符号数可以进一步分为原码、反码、补码形式:
原码
原码就是将正数的符号位用 0
表示,负数的符号位用 1
表示,数值用绝对值的二进制数形式表示。
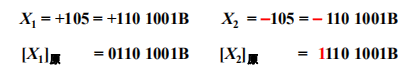
因此,真值 0 也会拥有 +0 和 -0
两种不同的表示形式:

注意:计算机当中,位
bit是二进制数据的最小单位,一位二进制数就是1比特(bit),通常将8位二进制数称为1字节(Byte),而4位二进制数称为半字节(Nibble/ˈnɪbl/)。
反码
原码简单易懂且便于转换为真值,但是实现加、减运算较为麻烦。为了简化计算机的处理过程,通常会将减法运算转换为加法运算,于是引进了补码的概念。由于补码与反码之间存在一定的换算关系,所以这里首先对反码进行介绍。
- 正数的反码与原码相同;
- 负数的反码是其正数的反码,但是符号位保持为
1,数值部分则按位取反;
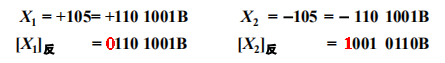
反码当中 0 同样拥有 +0 和 -0
两种不同的表示形式:
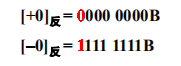
补码
减法运算 10 – 5 可以用 10 + 7
的加法运算来代替,而 5 和 7
相加正好是进位的模数 12,所以称 7 为
-5 对模 12 的补数,
也称为补码。
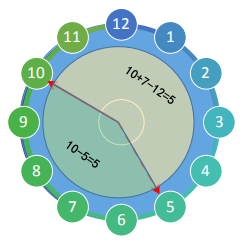
模是指一个计量系统的量程,例如时钟能够表示 \(1 \sim 12\),那么以 \(12\)
作为一个计数循环就被称为模。而四位二进制数能够表示
\(0000 \sim 1111\) 其模为
16,同理八位二进制数的模为 \(2^8
= 256\)。

所以,在舍弃进位的条件下,减去某数的计算可以采用加上这个数补码的计算来代替,该结论同样适用于二进制数的减法运算。
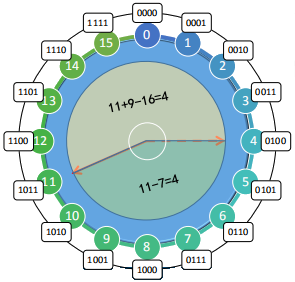
例如减法 \(1011 - 0111 = 0100\)
对应的十进制形式为 \(11 - 7 =
4\),在舍弃进位的条件下,可以采用 \(1011 + 1001 = 0100\)
形式代替,对应的十进制等式是 \(11 + 9 =
4\)。这是因为四位二进制数的模数为 16,而
9 恰好就是 -7 对模 16
的补码。
- 正数的补码与原码相同;
- 负数的补码是符号位为
1的负数,数值部分为其绝对值按位取反,并在最低位加1,即负数的补码等于其反码加上一;

注意,补码当中,真值 0 的表示是唯一的,即:
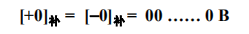
负数补数的简便求解方法:从右侧最低位向左侧最高位扫描,保留出现第一个
1 的位,后续的其它位全部按位取反,符号位保持不变。
▶【例题】使用八位二进制数,将 -90 用补码表示出来:
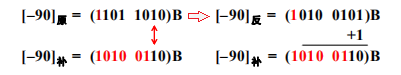
▶【例题】使用八位二进制数,将 -1 用补码表示出来:
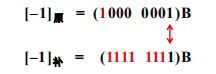
求解一个补码的补码,就可以将补码转换成原码,即 \([[x]_补]_补 = [x]_原\)。
▶【例题】求解 \([1010 1010]_补\) 的原码和真值?
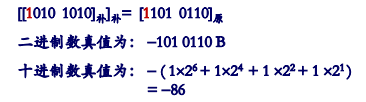
将补码当中所有等于 1
的位的权值相加(包括符号位,负数的符号位的权值被赋予负值),就可以得到其十进制数。
▶【例题】确定补数 \([0101\ 0110]_补\) 和 \([1010\ 1010]_补\) 的十进制值?
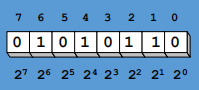
\[ [0101\ 0110]_补 = 1 \times 2^6 + 1 \times 2^4 + 1 \times 2^2 + 1 \times 2^1 = 64 + 16 + 4 + 2 = +86 \]
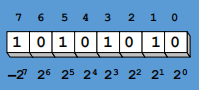
\[ [1010\ 1010]_补 = 1 \times (-2)^7 + 1 \times 2^5 + 1 \times 2^3 + 1 \times 2^1 = -128 + 32 + 8 + 2 = -86 \]
二进制代码
逻辑代数
组合逻辑电路
硬件描述语言 Verilog HDL
锁存器和触发器
时序逻辑电路
逻辑门电路
半导体存储器
可编程逻辑器件
脉冲波形的产生与变换
数模与模数转换器
现代数字逻辑电子技术概论