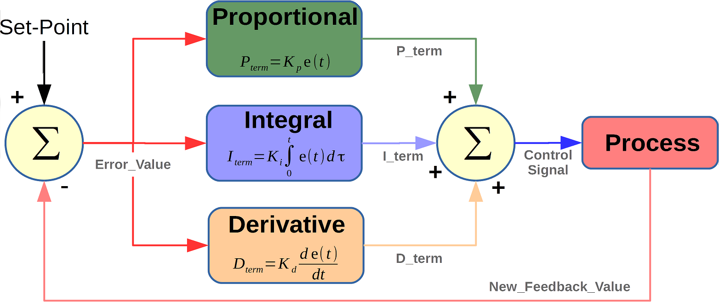
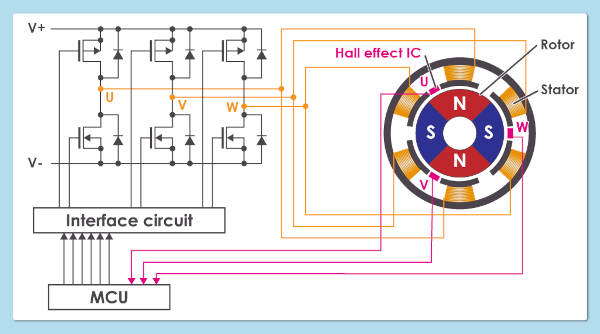
《实用电子元器件与电路基础》读书笔记

《实用电子元器件与电路基础》的英文原版书籍名称叫做《Practical Electronics for Inventors》，全书从电路基本原理入手，围绕各种类型的电子元器件进行了详细介绍。首先是阐述了基本的电路理论，然后重点讨论了包括 电阻、电容、电感、变压器 在内的基本元器件；接下来介绍了半导体电子技术，并且详细分析了 二极管、晶体管、晶闸管 等半导体元件的性能与参数，以及运算放大器、滤波电路、振荡电路、定时器、稳压电路与电源 等经典的模拟电路。

最后介绍了数字电子技术相关的内容，从基本的逻辑门电路入手，重点讨论了组合逻辑电路和时序逻辑电路，以及相关的 触发器，寄存器、计数器、缓冲器、锁存器、收发器，乃至于存储器与微控制器。除此之外，该书还简单介绍了线性函数、二次函数、指数/对数函数、三角函数、复数、微积分等数学预备知识。电子元器件的选型与运用是硬件工程师日常工作当中最为主要的内容，希望本篇文章能够对广大电子爱好者有所帮助。

数学预备知识

本章节内容主要用于归纳电子技术相关的常用数学基础知识。

希腊字母

英文	大写	小写	音标	英文	大写	小写	音标
Alpha	Α	α	/ˈælfə/	Beta	Β	β	/ˈbetə/
Gamma	Γ	γ	/ˈɡæmə/	Delta	∆	δ	/ˈdeltə/
Epsilon	Ε	ε	/ˈepsɪlɑːn/	Zeta	Ζ	ζ	/ˈzeɪtə/
Eta	Ε	η	/ˈiːtə/	Theta	Θ	θ	/ˈθeɪtə/
Iota	Ι	ι	/aɪˈoʊtə/	Kappa	Κ	κ	/ˈkæpə/
Lambda	Λ	λ	/ˈlæmdə/	Mu	Μ	µ	/mjuː/
Nu	Ν	ν	/njuː/	Xi	Ξ	ξ	/ksaɪ/
Omicron	Ο	ο	/ˈɑːməkrɑːn/	Pi	Π	π	/paɪ/
Rho	Ρ	ρ	/rəʊ/	Sigma	Σ	σ	/ˈsɪɡmə/
Tau	Τ	τ	/tɔːˌtaʊ/	Upsilon	Υ	υ	/ˈʊpsɪlɑːn/
Phi	Φ	φ	Phi	Chi	Χ	χ	/kaɪ/
Psi	Ψ	ψ	/psaɪ/	Omega	Ω	ω	/oʊˈmeɡə/

单位前缀

单位前缀	符号	乘方	音标	单位前缀	符号	乘方	音标
tera	T	\(× 10^{12}\)	/ˈterə/	milli	m	\(× 10^{−3}\)	/ˈmɪli/
giga	G	\(× 10^9\)	/ˈɡɪɡə/	micro	µ	\(× 10^{−6}\)	micro
mega	M	\(× 10^6\)	/ˈmeɡə/	nano	n	\(× 10^{−9}\)	/ˈnænoʊ/
kilo	k	\(× 10^3\)	/ˈkilo/	pico	p	\(× 10^{−12}\)	/ˈpiːkoʊ/
centi	c	\(× 10^{−2}\)	/ˈsentɪ/	-	-	-	-

线性函数

线性函数 \(y = mx + b\) 会在坐标轴上绘制出一条直线，这条直线的斜率 \(\frac{\Delta y}{\Delta x}\) 等于 \(m\)，垂直截距等于 \(b\)：

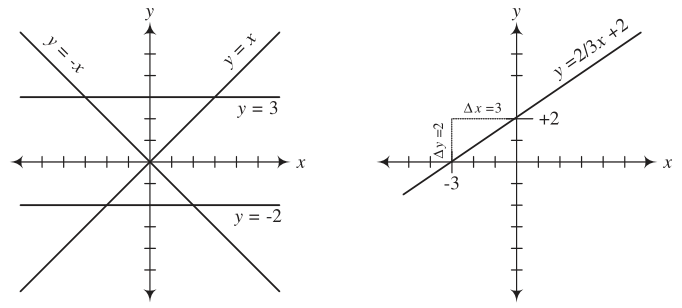
二次函数

二次函数 \(y = ax^2 + bx + c\) 会在坐标轴上绘制出一条抛物线，这条抛物线的大小受到 \(\alpha\) 值的影响，其横坐标为 \(-\frac{b}{2a}\)，而纵坐标为 \(-\frac{b^2}{a+c}\)，方程的根位于抛物线与横轴的交点，可以通过公式 \(x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\) 计算得到：

指数函数

形如 \(y=a^x（a>0，且a \neq 1）\) 的函数称为指数函数，其中的 \(x\) 为自变量，函数的定义域为 \(R\)。

\(x^0 = 1\)	\(\frac{1}{x^n} = x^{-n}\)	\(x^{1/n} = \sqrt[n]{x}\)	\(x^m \cdot x^n = x^{m+n}\)	\((xy)^n = x^n \cdot y^n\)	\((x^n)^m = x^{n \cdot m}\)

对数函数

如果 \(a^y = x（a>0，且 a \neq 1）\)，那么 \(y\) 就叫做以 \(a\) 为底 \(N\) 的对数，记作 \(y = log_a x\)，其中 \(a\) 称为对数的底数，而 \(x\) 称为真数。

• 常用对数：通常将以 10 为底的对数 \(\log_{10} x\) 记为 \(\lg x\)；
• 自然对数：通常将以无理数 2.71828... 作为底数的对数 \(\log_e x\) 记为 \(\ln x\)；

根据对数的定义，就可以得到对数与指数之间的关系：\(a^y = x（当 a>0 且 a \neq 1 时）\iff y = \log_a x\)。

\(\log_b 1 = 0\)	\(\log_b b = 1\)	\(\log_b 0 = \begin{cases} +\infty b < 1 \\ -\infty b > 1 \end{cases}\)
\(\log_b(x \cdot y) = \log_b x + \log_b y\)	\(\log_b(\frac{x}{y}) = \log_b x - \log_b y\)	\(\log_b (x^y) = y \log_b x\)

三角函数

对于半径为 \(R\) 的圆形，弧长 \(S\) 所对应的圆心角弧度 \(\theta = \frac{弧长 S}{半径 R}\)，此时 \(1 弧度 = \frac{180°}{\pi} = 57.296°\)，而 \(1° = \frac{\pi}{180°} = 0.17453 弧度\)：

当半径 \(R\) 从 \(x\) 正半轴开始逆时针方向旋转时，\(\theta\) 为正角，而顺时针方向旋转时，\(\theta\) 为负角。

\(\sin \theta = \frac{y}{R}\)	\(\cos \theta = \frac{x}{R}\)	\(\tan \theta = \frac{y}{x}\)	\(\cot \theta = \frac{x}{y} = \frac{1}{tan \theta}\)	\(\sec \theta = \frac{R}{x} = \frac{1}{\cos \theta}\)	\(\csc \theta = \frac{R}{y} = \frac{1}{\sin \theta}\)

正弦与余弦函数

下图为正弦函数曲线 \(y = A \sin \theta\)，为了方便改变函数的垂直水平位置、周期、相位，可以将其改写为 \(y = A \sin(Bx + C) + D\) 的形式，其中 \(A\) 表示幅值，而 \(2 \pi / B\) 表示周期 \(T\)，\(C\) 表示相移，\(D\) 表示垂直位移。

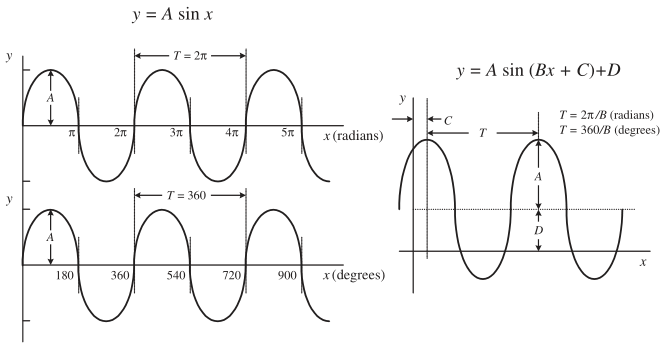
电子学当中，可以将电压表示为 \(V(t) = V_0 \sin(\omega t + \varPhi) + V_{dc}\)，其中 \(V_0\) 为峰值电压，\(V_{dc}\) 为直流分量，\(\varPhi\) 为相移，\(\omega\) 为角频率 \(rad/s\)。除此之外，余弦函数曲线 \(y = A \cos \theta\) 与 \(y = A \sin \theta\) 相差了 \(\frac{\pi}{2}\) 幅度或者 \(90°\) 度相移：

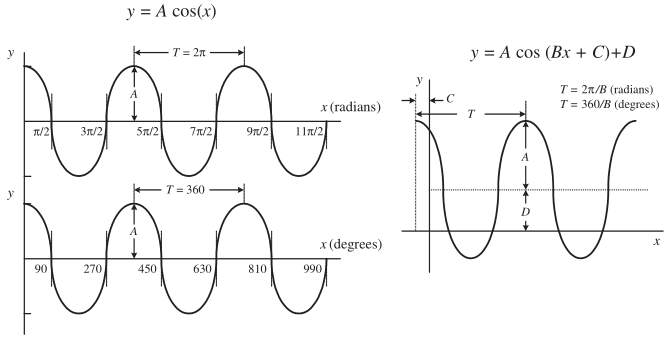
正弦函数与余弦函数之间的关系如下面表格所示：

\(\sin(\frac{\pi}{2} \pm x) = + \cos x\) 或者 \(\sin(90° \pm x) = + \cos x\)	\(\cos(\frac{\pi}{2} \pm x) = \pm \sin x\) 或者 \(\cos(90° \pm x) = \pm \sin x\)
\(\sin(\frac{3\pi}{2} \pm x) = - \cos x\) 或者 \(\sin(270° \pm x) = - \cos x\)	\(\cos(\frac{3\pi}{2} \pm x) = \pm \sin x\) 或者 \(\cos(270° \pm x) = \pm \sin x\)

斜率

斜率反映了直线相对于水平面的倾斜度，一条直线与某平面直角坐标系横坐标轴的正半轴所形成角的正切值，就等于该直线的斜率。

\[ 直线的斜率 = \frac{直线某点在\ y\ 轴的变化量\ \Delta y}{直线某点在\ x\ 轴的变化量\ \Delta x} \]

假设函数 \(f(x)\) 的图形为一条曲线，此时存在着一个点沿着这条曲线移动，经过该点绘制切线，当该点沿着曲线运动时，切线的斜率不断发生变化。实际生活当中，切线的斜率有着极为重要的意义，例如：

• 当绘制某个物体相对于时间的位移曲线时，曲线上某个时间点的切线斜率，就表示了该物体在该时间点的瞬时速度；
• 基于时间的充电曲线当中，时刻 \(t\) 位置的斜率就表示该时刻的瞬时电流；

微分学

微分学作为作为计算斜率的途径之一，可以用于计算曲线上任意一点位置的切线斜率。例如函数 \(y = x^2\)，通过微分计算可以得到 \(y\) 的导数 \(y' = \frac{dy}{dx} = 2x\)，通过它可以获得曲线 \(y\) 上任意一点位置的斜率。如果此时需要求解 \(x = 2\) 位置的斜率，将 \(x = 2\) 代入至 \(\frac{dy}{dx}\) 表达式，就可以得到斜率等于 \(4\)。

当计算某个函数的导数时，假设 \(P(x, y)\) 为曲线 \(y = f(x)\) 上面的一点，而 \(Q(x + \Delta x, y + \Delta y)\) 为曲线上的另外一点，此时 \(P\) 点与 \(Q\) 点之间的直线斜率为 \(\frac{f(x + \Delta x) - f(x)}{\Delta x}\)：

将具体函数代入上面等式，例如对于函数 \(f(x) = x^2\)，那么 \(f(x + \Delta x) = (x + \Delta x)^2\)，此时完整的表达式可以记为 \(\frac{[(x + \Delta x)^2 - x^2]}{\Delta x}\)。接下来固定 \(x\) 的值，令 \(\Delta x\) 趋近于 0，如果斜率趋近于某一个只依赖于 \(x\) 的值，则称该值为曲线在 \(P\) 点处的斜率。

曲线在 \(P\) 点位置的斜率是一个关于 \(x\) 的函数，定义域为极限里存在的每个 \(x\) 值，那么斜率就可以表示为 \(f'(x)\)、\(\frac{dy}{dx}\)、\(\frac{df}{dx}\) 三种形式，这三种表达方式均称为 \(f(x)\) 的导数：

\[ f'(x) = \frac{dy}{dx} = \lim_{\Delta x \rightarrow 0} \frac{f(x + \Delta x) - f(x)}{\Delta x} \]

对于上述示例当中的函数 \(f(x) = x^2\)，求取极限之后，可以得到其导数为 \(f'(x) = \frac{dy}{dx} = 2x\)。实际计算当中，使用上述极限公式计算较为繁琐，通常会直接应用下面表格当中的求导法则与函数导数：

\(\frac{d}{dx} a = 0\)	\(\frac{d}{dx} x^n = nx^{n - 1}\)	\(\frac{d}{dx} e^x = e^x\)	\(\frac{d}{dx} \ln x = \frac{1}{x}\)	\(\frac{d}{dx} \sin x = \cos x\)
\(\frac{d}{dx} \cos x = -\sin x\)	\(\frac{d}{dx} au(x) = a \frac{d}{dx} u(x)\)	\(\frac{d}{dx}(u + v) = \frac{du}{dx} + \frac{dv}{dx}\)	\(\frac{d}{dx}\Bigl(\frac{u}{v}\Bigl) = \frac{v(du/dx) - u(dv/dx)}{v^2}\)	\(\frac{d}{dx} \left \lbrace u(v(x)) \right \rbrace = \frac{du}{dx} \cdot \frac{dv}{dx}\)

注意：上面表格当中的 \(a\) 和 \(n\) 是常数，而 \(u\) 和 \(v\) 表示函数。

• 导数是函数图像在某一点位置的斜率，即纵坐标增量 \(\Delta y\) 与横坐标增量 \(\Delta x\) 的比值；
• 微分是指函数图像在某一点处的切线在横坐标取得增量 \(\Delta x\) 以后，纵坐标所相应取得的增量；

积分学

微分学的目标是寻找函数的导数，而积分学的任务则是寻找导数的原函数。通常约定 \(y = f(x)\) 形式为函数，而 \(\frac{dy}{dx} = \frac{df(x)}{dx}\) 形式为导数，形如 \(\int dy = \int f(x)dx\) 的称为积分。其中，\(\int\) 称为积分符号，而 \(f(x)\) 称为被积函数，\(dx\) 称为积分变量。实质上积分可以被视为一个求和计算的过程，例如求解下图以曲线作为边界的阴影区域面积：

已知等式 \(\frac{dy}{dx} = f(x)\)，通过积分计算就可以得到 \(y\)：

\[ \frac{dy}{dx} = f(x) \implies \int dy = \int f(x)dx \xrightarrow{对等式两侧进行积分} y \pm C = \int f(x) dx \implies y = \int f(x) dx + C \]

最后推导出等式 \(\int dy = y \pm C\)，通过逆运算可知任何 \(y \pm G\) 形式的函数，求导之后均等于 \(y\)。其中 \(C\) 的值可正可负，习惯上采用等号左侧加 \(C\) 的形式，这种形式的积分称为不定积分。例如已知 \(\frac{dy}{dx} = 2\)，可以通过如下推导过程求解得到 \(y\)：

\[ dy = 2dx \implies \int dy = \int 2dx \implies y = 2x + C \]

实际情况经常期望得到一个不包含常数的确定解，为了去掉常数项，就需要利用到边界条件。这里仍然以 \(\frac{dy}{dx} = 2\) 为例，如果只关注 \(\frac{dy}{dx}\) 在区间 \(1 \sim 5\) 范围内的值，就可以利用定积分来进行计算：

\[ y = \int^{b}_{a} f(x) dx = F(x) {\vert}^b_a = F(b) - F(a) \]

上面公式当中的 \(F\) 代表不含积分常数的定积分，而 \(a\) 和 \(b\) 限定了 \(F\) 当中 \(x\) 的取值区间，将已知条件代入方程可以得到：

\[ y = \int^{5}_{1} 2dx = 2x {\vert}^5_1 = 2 \times 5 - 2 \times 1 = 8 \]

对于更为复杂的函数，求解积分需要耗费较长时间推导其原函数。实际工作当中，更多会直接应用下面表格当中的积分公式进行分析讨论：

\(\int dx = x + C\)	\(\int a f(x) dx = a \int f(x) dx\)	\(\int(du(x) \pm dv(x)) = \int du(x) \pm \int dv(x)\)	\(\int udv = uv - \int vdu\)
\(\int u^n du = \frac{u^{n+1}}{u+1} + C \ (n \neq 1)\)	\(\int \frac{1}{u} du = \ln u + C\)	\(\int \ln xdx = x \ln x - x + C\)	\(\int sin xdx = -cos x + C\)
\(\int \cos xdx = \sin x + C\)	\(\int x \sin xdx = \sin x - x \cos x + C\)	\(\int x \cos xdx = \cos x + x \sin x + C\)	\(\sin x \cos x = \frac{1}{2} \sin^2 x + C\)
\(\int e^u dx = e^u + C\)

注意：上面表格当中的 \(u\) 和 \(v\) 分别表示 \(x\) 的函数。

复数

利用复数及其对应的算术运算法则来模拟与求解正弦电路相关的问题，可以避免复杂的微分方程计算过程。复数 \(z = a + ib\) 主要由实部和虚部两部分所共同组成：

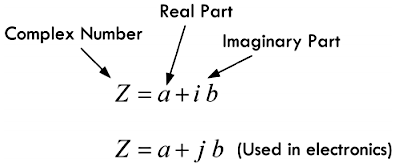
上面公式当中的 a 称为实部，b 称为虚部，i 称为虚数单位（\(i = \sqrt{-1}\)）。电路分析当中，为了避免虚数单位 i 与电流符号 \(i\) 相互混淆，而改用 j 来代替虚数单位 i。除此之外，复数还可以在采用直角坐标系上的图像（下图左侧）来进行表示，其中横轴表示实部 a，而纵轴表示虚部 b（下图右侧），即复数的直角坐标系形式：

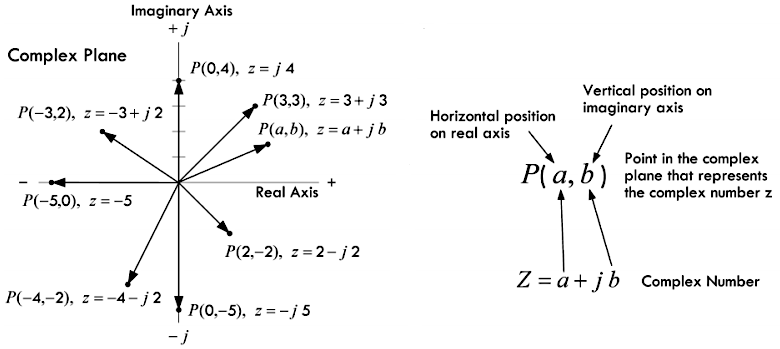
注意：可以将直角坐标系里的复数视为一个由 0 指向 P 点的矢量，对应的模值为 \(r = \sqrt{a^2 + b^2}\)，其与正实轴之间的夹角 \(\theta = \arctan(\frac{b}{a})\)。

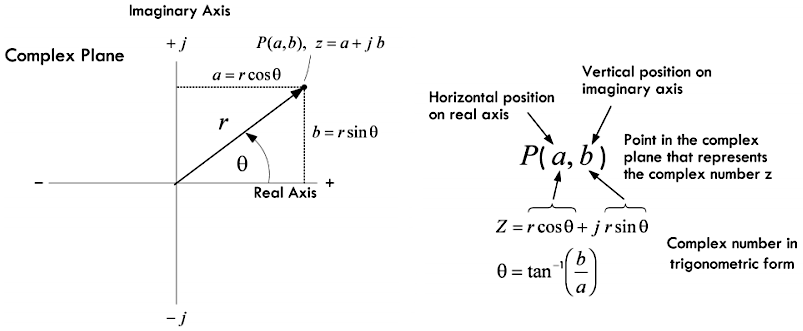
将复数用于电路分析，必须对其进行形式上的改变。将 a 更换为 \(r \cdot \cos \theta\)，而 b 更换为 \(r \cdot \sin \theta\)，进而得到 \(z = r \cdot \cos \theta + j \times r \cdot \sin \theta\)，这就是复数的三角形式：

复数的三角形式满足 \(e^{j \theta} = \cos \theta + j \sin \theta\) 的关系，首先分别对 \(e^{j \theta}\)、\(\cos \theta\)、\(j \sin \theta\) 取幂级数，然后将 \(\cos \theta\) 与 \(j \sin \theta\) 的幂级数相加，最后就可以证明其结果与 \(e^{j \theta}\) 的幂级数相等，从而就可以得到复数的指数形式：

\[ z = r \cdot e^{j \theta} \]

上面的复数指数形式，还可以进一步简写为由矢量 \(r\) 与角度 \(\theta\) 两部分组成的极坐标形式：

\[ z = r \cdot \angle \theta \]

注意：复数的极坐标形式可以视为其指数形式的简写，相对而言，极坐标形式更为直观，计算起来也更加便捷。

终上所述，一共获得了复数的四种基本表示形式（标准形式、直角坐标系形式、三角形式、指数形式），每一种形式在电路分析当中都具有相应的特殊用途：

\[ \begin{aligned} 复数的直角坐标系形式：&z = a + ib \\ 复数的三角形式：&z = r \cdot \cos \theta + j \times r \cdot \sin \theta \\ 复数的极坐标形式：&z = r \cdot \angle \theta \\ 复数的指数形式：&z = r \cdot e^{j \theta} \end{aligned} \]

下图直观的展示了复数在各种形式之间的转换关系：

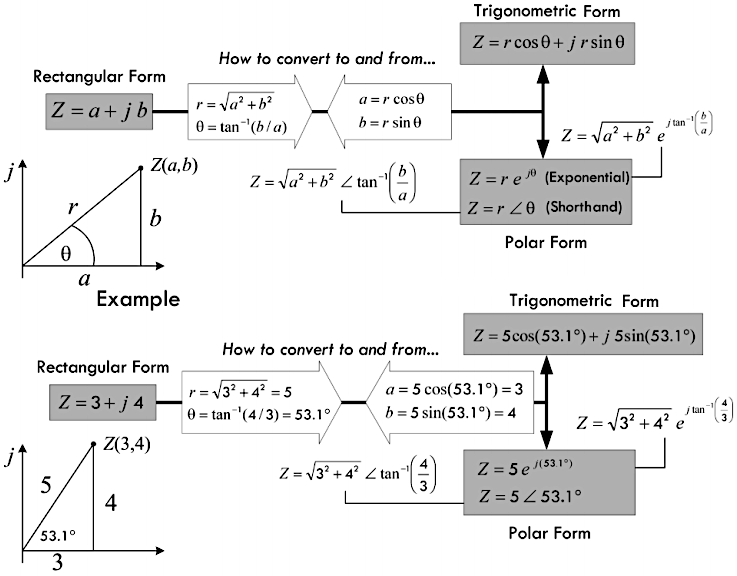
如下的表格，比较全面的总结了复数在各种形式下的加、减、乘、除四则运算法则：

而接下来的表格，展示了复数在计算过程当中，一些经常被使用到的关系方程式：

\(X(度) = \frac{180°}{\pi} X(弧度)\)	\(X(弧度) = \frac{\pi}{180°} X(度)\)
\(j = \sqrt{-1}\)	\(j^2 = -1\)	\(\frac{1}{j} = -j\)	\(\frac{1}{A + jB} = \frac{A - jB}{A^2 + B^2}\)
\(e^{j(0°)} = 1\)	\(e^{j(90°)} = j\)	\(e^{j(180°)} = -1\)	\(e^{j(270°)} = -j\)	\(e^{j(360°)} = 1\)
\(1 \angle 0° = 1\)	\(1 \angle 90° = j\)	\(1 \angle 180° = -1\)	\(1 \angle 270° = -j\)	\(1 \angle 360° = 1\)
\(Z^2 = (re^{j \theta})^2 = r^2 e^{j2 \theta}\)	\(Z^2 = (r \angle \theta)^2 = r^2 \angle 2 \theta\)

注意：如果需要在电路分析过程当中进行复数运算，那么可以直接套用上述公式简化计算量。

▶【例题】应用复数的四则混合运算，求解下面复数的直角坐标形式与极坐标形式结果 ？

\[ \frac{(2 + j5)+(3 - j10)}{(3 + j4)(2 + j8)} \]

◉【解】直接运用之前表格当中列出的关系式，就可以得到下面的推导过程：

\[ \frac{(2 + j5)+(3 - j10)}{(3 + j4)(2 + j8)} \implies \frac{5 - j5}{(3 + j4)(2 + j8)} \implies \frac{7.07 \angle 45.0°}{(5 \angle 53.1°)(8.25 \angle 76.0°)} \implies \frac{7.07 \angle 45.0°}{41.25 \angle 129.1°} \implies 0.17 \angle - 84.1° \]

◉【解】上述步骤所获得的计算结果，可以按照题设要求转换为三角形式或者直角坐标形式：

\[ 0.17 \angle −84.1° = 0.17 \cos (−84.1°) + j0.17 \sin (−84.1°) = 0.017 − j0.17 \]

注意：进行复数的除法或者乘法运算时，最佳实践是将复数转换为指数形式。而对于复数的加法与减法运算，最佳实践是将其转换为直角坐标系形式。

形如等式 \(|Z| = \sqrt{(R_e Z)^2 + (I_m Z)^2}\) 或者 \(arg(Z) = \arctan(\frac{I_m Z}{R_e Z}) = \tan^{-1} (\frac{I_m Z}{R_e Z})\) 表示的依然是一个复数，该等式当中的 \(|Z|\) 是复数的幅值或者模，\(I_m Z\) 是复数的虚部，而 \(arg(Z)\) 表示的是 \(Z\) 的幅角或者 \(\theta\) 相位角。如果按照这个对应规则，那么对于复数 \(Z = 3 + j4\) 而言：

\[ \begin{cases} R_e Z = 3 \\ I_m Z = 4 \\ |Z| = \sqrt{(3)^2 + (4)^2} = 5 \\ arg(Z) = \arctan(\frac{4}{3}) = 53.1° \end{cases} \]

注意：电路分析过程当中，引入复数的概念，可以有效简化交流电路的分析计算过程。

电路基础

电流

电流是单位时间内通过某一横截面 A 的总电荷，这里的横截面可以理解为导体上的一个薄片：

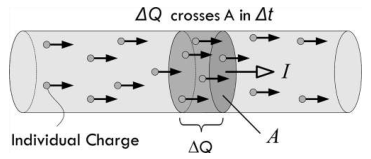
如果在 \(\Delta t\) 时间内，通过某一横截面的电荷量为 \(\Delta Q\)，那么就可以定义平均电流 \(I_{ave}\) 等于：

\[ I_{ave} = \frac{\Delta Q}{\Delta t} \]

如果电流随着时间变化，那么可以定义 \(\Delta \rightarrow 0\) 时的电流值为瞬时电流，即瞬时电流是电荷通过某一横截面的变化率：

\[ I = \lim_{\Delta \rightarrow 0} \frac{\Delta Q}{\Delta t} = \frac{dQ}{dt} \]

电流的单位称为安培 A，其值等于 1C/s 库伦每秒，除此之外，常用的单位还有毫安、微安、纳安：

\[ \begin{aligned} 1A &= 1C/s \\ 1 mA &= 10^{-3}A \\ 1 \mu A &= 10^{-6}A \\ 1 nA &= 10^{-9}A \\ \end{aligned} \]

电流是由导体内自由电子的定向移动而形成的，每个自由电子的电荷量为 \(-1.602 \times 10^{-19} C\)。由于导体当中的质子与电子数量相等符号相反，因而整体呈现电中性：

\[ \begin{cases} Q_{electron} &= -1.602 \times 10^{-19} C \\ Q_{proton} &= +1.602 \times 10^{-19} C \end{cases} \]

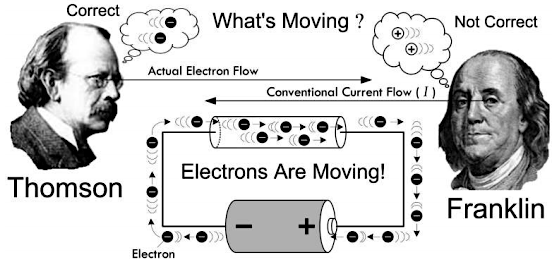
最早富兰克林（Franklin）将正电荷运动的方向定义为电流方向，后来汤姆逊（Thomson）纠正了这一观点，认为负电荷（自由电子）运动的方向才是电流的方向，但是无论哪种方向，对于电路的分析计算结果都不会产生实质性影响。

电压

电路两点之间存在电压才能够形成电流，导体两端的电压提供了推动导体当中自由电子运动的电动势（EMF，Electro- Motive Force），电压有时候也被称为电势差或者电位，但是后者更偏向于相对位能的概念。

实质上，电压表示的是单位电荷在两点之间的位能差，是衡量电场力做功能力的物理量。如果两点之间的电压为 1V 伏特，相当于将 1C 库仑的电荷从一点移动到另外一点所需要做的功为 1J 焦耳：

\[ 电压 V = \frac{功率 U}{电荷量 q} \implies 1 V 伏特 = \frac{1 J 焦耳}{1 C 库仑} \]

电子学当中，通常会使用功率 \(P\)（每秒钟为电路提供的能量，单位为瓦特 W）来定义电压的单位伏特：

\[ 功率 P = 电压 V \times 电流 I \implies 1 V 伏特 = \frac{1 W 瓦特}{1 A 安培} \]

电阻

欧姆定律

欧姆定律是指物体两端的电阻 \(R\) 等于两端电压 \(V\) 与通过电流 \(I\) 之比，单位为欧姆 Ω，

\[ 电阻 R = \frac{电压 V}{电流 I} \implies 1 Ω 欧姆 = \frac{1 V 伏特}{1 A 安培} \]

欧姆定律只适用于欧姆材料，即在所能承受的电压范围之内，该材料的电阻为一个常数。由于非欧姆材料的电阻不是常数，所以并不会遵循欧姆定律。

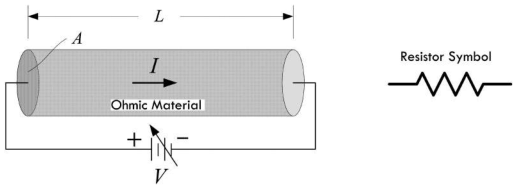
通常情况下，欧姆定律被写作 \(V = I \times R\) 的形式，即使用电阻与电流来定义电压。欧姆材料的电阻 \(R\) 与欧姆定律当中的电压 \(V\) 无关。换而言之，就是不能使用电阻和电流来定义电压，而只能使用电压与电流来定义电阻。

电阻率 & 电导率

电阻率 \(\rho\) 反映了物体阻碍电流的能力，属于材料的固有特性，其单位为欧姆 \(\cdot\) 米（\(Ω \cdot m\)）

\[ 电阻率 \rho = 电阻 R \frac{横截面积 A}{长度 L} \]

电导率 \(\sigma\) 反映了物体通过电流的能力，同样也是材料的固有特性，其值等于电阻率的倒数，单位为西门子 \(S = (Ω \cdot m)^{-1}\)

\[ 电导率 \sigma = \frac{1}{电阻率 \rho} \]

下面的表格里，分别列举出了一些常见材料的电阻率与电导率：

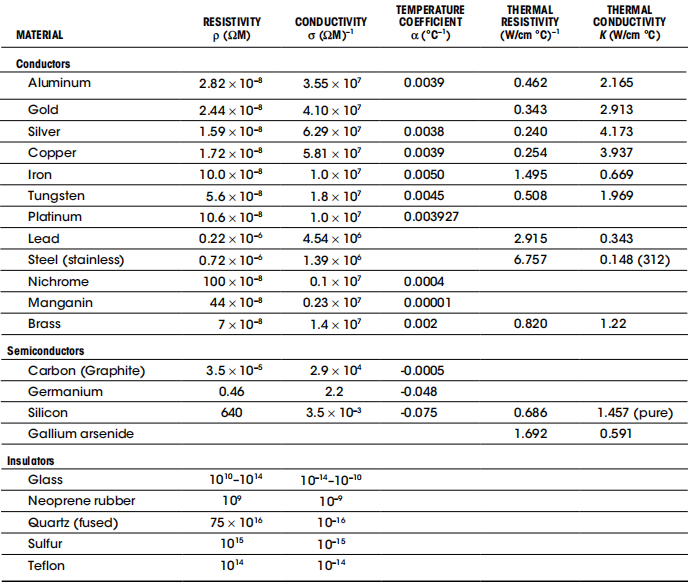
注意：大部分金属的电导率会随着温度的升高而增大，这是由于温度升高会导致材料晶格当中原子的振动，从而阻碍导体内部电子的漂移运动。

欧姆热

理想电阻的情况下，可以认为其全部功率都被转化为热能，将欧姆定律 \(I = \frac{V}{R}\) 或者 \(V = IR\) 代入功率的表达式 \(P = VI\) 当中，就可以得到功率 \(P\) 所消耗的热能，即欧姆热或者焦耳热：

\[ \begin{aligned} 功率 P = 电压 V \times 电流 I &= 电压 V \times \frac{电压 V}{电阻 R} = \frac{V^2}{R} \\ 功率 P = 电压 V \times 电流 I &= (电流 I \times 电阻 R) \times 电流 I = I^2 \times R \end{aligned} \]

AWG 导线规格

导线的尺寸可以使用导线规格来进行表示，国际上经常采用美国导线规格（AWG，American Wire Gauge）作为通用标准，该标准下较小的规格数目对应着较大直径的导线：

下面的表格列举了铜导线的常见 AWG 规格，其中单位 \(1 mil 密尔 = 0.0254mm 毫米\)：

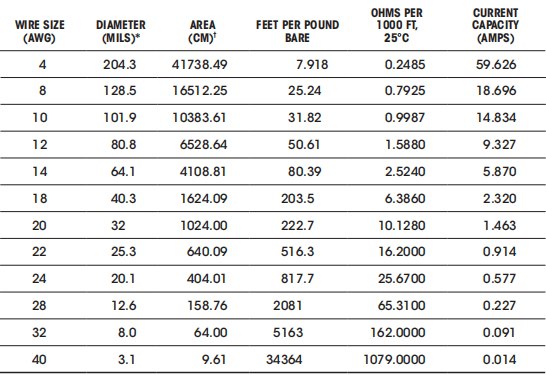
注意：圆密尔 CM 是一个面积单位，表示的是直径为 1 mil 的圆面积。

接地

接地分类

通常会将电路当中的一点定义为 0V 参考点，并以此作为测量电路上其它各点电压的基准，该点通常被称为接地点或者电流返回端，采用下图符号进行表示：

注意：物理上的接地，是指将导体埋入大地 \(8 英尺 = 2.4384 米\) 以上。

除此之外，为避免发生混淆，可以采用含义更为明确的 大地、框架底座接地(功率接地)、模拟数字接地、电压参考点 符号：

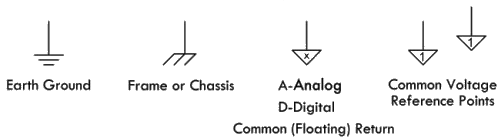
注意：除了作为零电压参考点使用之外，接地系统的另外一个重要作用是为无线电设备产生的杂散射频电流提供一条流入大地的低阻通路，称为射频接地。

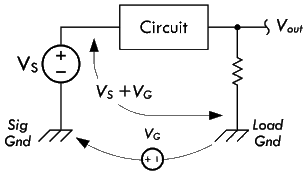
单点接地

较为复杂的 PCB 设计当中，信号噪声产生的最普遍原因是由于没有良好的接地，如果将 PCB 线路当中的某些点作为接地点，那么接地线的内阻会导致这些接地点之间存在着电位差，从而形成糟糕的接地回路，导致电压读数产生误差。

下图给出了这个问题的说明，图中两个分离的底座接地，\(V_G\) 表示信号接地端与负载接地端之间的电压，\(V_S\) 为负载接地端与信号输出端之间的电压，此时会得到一个错误的电压 \(V_S + V_G\)：

解决该问题的方法是采用下图所示的单点接地，即为了避免在电路当中产生接地回路，而将所有电路的接地端都连接至一个点：

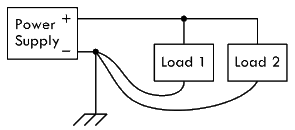
理论上这是一个很棒的方法，但是由于 PCB 电路的接地端数量通常会比较多，实际布线操作很难将其全部连接至一个点，替代的方法是采用接地母线，也就是采用较宽的铜制导线，以便承受回流至电源的全部负载电流。由于接地母线可以按需进行延长，所以布线时进行接地操作会较为方便：

PCB 电路板通常会划分为模拟电路和数字电路两个部分，通常情况下会将两者分别进行接地处理，最后再将其接地点连接起来进行单点接地，作用是防止电路当中的接地回路产生电流噪声。

• 数字电路当中，当信号发生改变时会在电路中产生冲击电流；
• 模拟电路当中，当负载电流发生变化或者改变方向时也会产生冲击电流；

上述两种情况下，如果电流发生改变，则根据欧姆定律，接地回路上的阻抗电压也将会随之改变，从而导致系统参考点（通常选择在电源引出端）相对于接地面的电压也发生变化。接地回路上的阻抗由电阻、容抗、感抗共同组成，其中电阻与感抗起到主要作用。

• 如果接地回路当中经过的是直流电流，则电阻起到主要作用，并且产生一个直流偏置电压；
• 如果接地回路当中经过的是交流电流，则同时产生电阻、感抗、容抗，进而产生一个高频交流电压；

上述两种情况下，局部电路的电压变化都会导致噪声的出现，而减少噪声的最好办法就是先将模拟接地和数字接地分开，最后再进行单接地点。

串并联电路

电路主要存在串联与并联两种基本连结方式，其中串联的负载具有分压的作用，而并联的负载具有分流的作用：

静态电路理论

电阻与欧姆定律

电阻可以限制电路当中电流的流动，或者是在电路两端形成电压，主要分为固定电阻与可变电阻两大类型，其电路表示符号如下所示：

如果在一个电阻的两端添加直流电压，那么运用欧姆定律就可以计算出经过这个电阻的电流：

\[ 电压 V = 电流 I \times 电阻 R \]

如果要计算出该电阻欧姆热所消耗的功率，可以将欧姆定律代入功率的计算公式：

\[ 功率损耗 P = 电流 I \times 电压 V = \frac{电压 V^2}{电阻 R} = I^2 R \]

注意：设计电路的时候，电阻的实际功率不能超过其最大额定功率，否则会损坏电阻。典型的电阻器额定功率值有 1/8W、1/4W、1/2W、1W。生产环境下，电阻的额定功率应当至少大于期望值的两倍以上。

假设下图当中的电阻可以调节阻值，并且电源电压恒定为 5V。此时，增大电阻就会导致电流与功率的减小；而当减小电阻时，电流与功率又会增加，所以选用阻值较小的电阻器时，必须适当提高电阻器的额定功率参数标准。

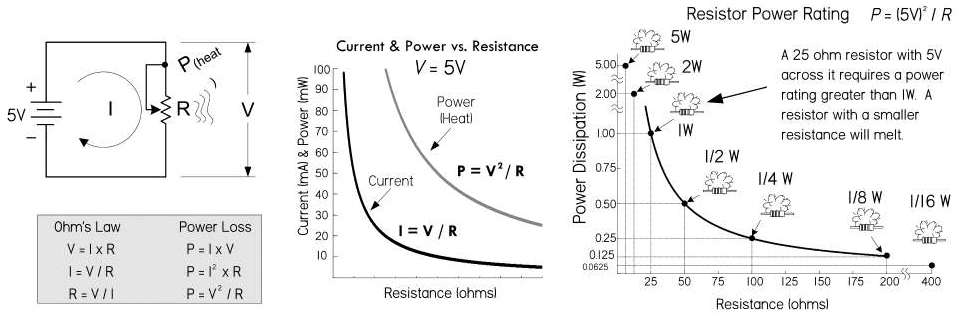
电阻的并联

当多个电阻器进行并联时，每一个并电阻器上的电压相同，但是通过的电流会跟随阻值进行变化。并联电路的总电阻，小于各个并联电阻的阻值，并联电阻器的总电阻计算公式如下面所示：

\[ R_{total} = \frac{1}{\frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + \frac{1}{R_4} + \frac{1}{R_5} + ...} \]

如果仅仅只有两个电阻并联在一起，则其总电阻的计算公式可以被简化为下面的形式：

\[ R_{total} = \frac{R_1 \times R_2}{R_1 + R_2} \]

1. 根据基尔霍夫电流定律得到总电流 \(I_{total} = I_1 + I_2 + I_3 + ... + I_n\)；
2. 根据欧姆定律可以进一步得到 \(I_{total} = \frac{V_1}{R_1} + \frac{V_2}{R_2} + \frac{V_3}{R_3} + ... + \frac{V_n}{R_n}\)；
3. 由于并联电阻上的电压 \(V_n\) 都等于总电压 \(V_{total}\)，代入以后得到 \(I_{total} = \frac{V_{total}}{R_1} + \frac{V_{total}}{R_2} + \frac{V_{total}}{R_3} + ... + \frac{V_{total}}{R_n}\)；
4. 提取公因数 \(V_{total}\) 进行化简 \(I_{total} = V_{total}(\frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + ... + \frac{1}{R_n})\)；
5. 继续将等式变换为欧姆定律的形式 \(\frac{1}{\frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + ... + \frac{1}{R_n}} = \frac{V_{total}}{I_{total}}\)
6. 此时 \(\frac{1}{\frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + ... + \frac{1}{R_n}}\) 部分就是等效总电阻 \(R_{total}\) 的计算公式；

电阻的串联

当多个电阻器进行串联时，总电阻等于各个串联电阻之和，流经每一个串联电阻器的电流相同，而电压则跟随阻值进行变化，串联电阻器的总电阻 \(R_{total}\) 计算公式如下所示：

\[ R_{total} = R_1 + R_2 + R_3 + R_4 + R_5 ... + R_n \]

1. 根据基尔霍夫电压定律得到总电压 \(V_{total} = V_1 + V_2 + V_3 + ... + V_n\)；
2. 由于经过每一个串联电阻器的电流 \(I\) 都相同，根据欧姆定律可以进一步得到 \(I \times R_{total} = I \cdot R_1 + I \cdot R_2 + I \cdot R_3 + ... + I \cdot R_n\)；
3. 消除等式两边的公因数 \(I\)，就能够得到等效总电阻的计算公式 \(R_{total} = R_1 + R_2 + R_3 + ... + R_n\)；

注意：电阻上标记的最大額定功率不非电阻器实际消耗的功率。流过每一个串联电阻上经过的电流都相同，但是每一个串联电阻器上的电压会随阻值的不同而变化。

电阻分压电路

下图是一个串联电阻分压电路，其中 \(V_{in}\) 为输入电压，而 \(V_2\) 为输出电压 \(V_{out}\)：

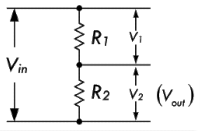
可以看到，每一个串联电阻上的电压与其电阻值的大小成正比，上述电路对应的分压公式如下所示：

\[ \begin{aligned} V_1 = \frac{R_1}{R_1 + R_2} \times V_{in} \\ V_2 = \frac{R_2}{R_1 + R_2} \times V_{in} \\ \end{aligned} \]

10％ 规则是设计分压电路的时候，选择电阻 \(R_1\) 与 \(R_2\) 的一种标准方法，该方法综合考虑了负载的影响与负载损耗功率最小的问题。

1. 首先是选择 \(R_2\)，使得 \(R_2\) 上的电流 \(I_2\) 为预期负载电流的 10％，此时就称 \(R_2\) 为泄漏电阻 \(R_{bleed}\)，而 \(R_2\) 上的电流称为泄漏电流 \(I_{bleed}\)；
2. 然后计算出通过电阻器的总电流，根据欧姆定律就可以计算得到电阻 \(R_1\) 的取值；

▶【例题】下图是一个 10V 的电压源，如果要将一个额定电压为 3V，额定电流为 9.1mA 的设备连接到电源上，请为该电路的负载设计一个分压器？

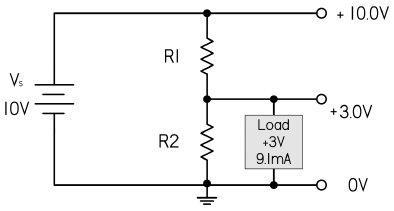
◉【解】根据题设条件，可以分别计算得到泄露电流 \(I_{bleed}\) 与泄露电阻 \(R_{bleed}\)：

\[ \begin{cases} I_{bleed} = I_2 = 9.1 mA \times 10\% = 0.91mA \\ R_{bleed} = R_2 = 3V \times 0.0091A = 3197Ω \end{cases} \]

◉【解】考虑到真实电阻器的阻值带有误差，\(R_2\) 需要选择一个阻值接近于上述计算值的 \(3300Ω\) 电阻器。接下来，确定电阻 \(R_1\)，使其输出电压维持在 3V。首先计算出通过电阻器 \(I_1\) 的总电流，然后根据欧姆定律计算出 \(R_1\)：

\[ I_1 = I_2 + I_{load} = 0.91 mA + 9.1mA = 10.0mA = 0.01 A \implies R_1 = \frac{10V - 3V}{0.01 A} = 700Ω \]

◉【解】最后，再来着手确定两个电阻器所需的额定功率：

\[ \begin{cases} P_1 = \frac{V_1^2}{R_1} = \frac{(7V)^2}{700Ω} = 0.07W = 70mW \\ P_{R2} = \frac{V_2^2}{R_2} = \frac{(3V)^2}{3300Ω} = 0.003W = 3mW \end{cases} \]

◉【解】根据上述推导过程就可以知道，选择额定功率小于 1/4W 的电阻器就可以满足需求。

▶【例题】已知负载 1（75V，30mA）、负载 2（50V，10mA)、负载 3（25V，10mA），请采用 10% 规则设计一个可以分别为三个负载提供功率的多项分压器？

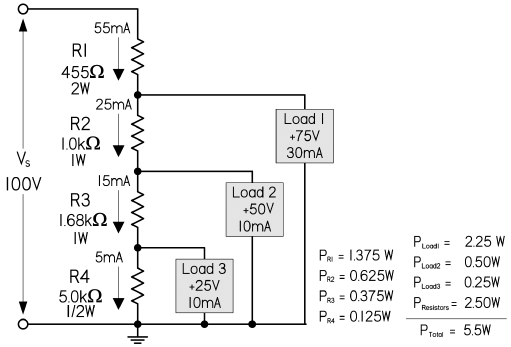
◉【解】运用 10％ 规则确定分压电阻的关键是计算泄漏电流 \(I_{R4}\)，其值等于总电流的 10%，也就是总电流的 0.1 倍，具体计算步骤如下所示：

\[ I_{R4} = 0.1 \times (10mA + 10mA + 30mA) = 5mA \]

◉【解】接下来，再根据欧姆定律获得泄露电阻 \(R_4\) 的阻值：

\[ R_4 = \frac{(25V - 0V)}{0.005A } = 5000Ω \]

◉【解】此时，流过电阻 \(R_3\) 的电流，等于经过电阻 \(R_4\) 的电流与经过负载 3 的电流之和：

\[ I_{R3} = I_{R4} + I_{load3} = 5mA + 10mA = 15mA \]

◉【解】然后，应用欧姆定律和负载 2 与负载 3 之间的电位差来求解电阻 \(R_3\)：

\[ R_3 = \frac{(50V - 25V)}{0.015A} \approx 1667Ω \]

◉【解】类似的，根据经过电阻 \(R_2\) 上的电流，运用欧姆定律，就可以求解得到电阻 \(R_2\)：

\[ I_{R2} = I_{R3} + I_{load2} = 15mA + 10mA = 25mA \implies R_2 = \frac{(75V - 50V)}{0.025A} = 1000Ω \]

◉【解】同样根据经过电阻 \(R_1\) 上的电流，根据欧姆定律，还可以求解得到电阻 \(R_1\)：

\[ I_{R1} = I_{R2} + I_{load1} = 25mA + 30mA = 55mA \implies R_2 = \frac{(100V - 75V)}{0.055A} = 455Ω \]

注意：虽然分压器结构简单，但是不能随意调节参数。如果一个负载的电阻或者电源电压发生改变，那么所有负载的电压都会发生变化。相比较而言，采用基于运算放大器的电压调整器是更佳选择。

理想电压源

理想电压源是一个双端元件，其两个端子之间的电压保持着一个固定值。如果将一个可变的负载连接到一个理想电压源，那么无论负载的电阻值如何进行变化，理想电压源的电压始终保持不变，而根据 \(I = \frac{V}{R}\)，当电压 \(V\) 固定时，电流 \(I\) 随着电阻 \(R\) 的变化而变化。当电阻的阻值变为零时，理想电压源的电流就会变为无穷大。

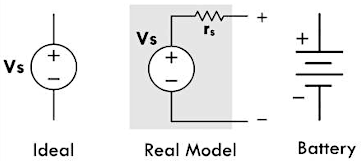
现实世界并不存在能够提供无穷大电流的电源设备，如果直接用导线将理想电压源的两端连接起来，那么电路当中产生的电流将会致使导线熔化，为了避免出现类似的理论难题，必须定义一个由理想电压源与电阻串联组成的实际电压源，其提供的最大电流为一个有限值。其中的电阻作为电源内阻，表示电压源并非一个理想的导体，可以降低电压源两端的电压，具体降低的数值取决于电压源两端的电压与经过的电流（或者负载电阻的大小）。

上图的电路当中，将一个理想电压源的两端开路，此时由于电路没有形成回路，电源内阻上面没有电流经过，因而不会产生电压，电压源的端电压 \(V_T\) 等于理想电压源的电压 \(V_S\)。当将一个负载电阻 \(R_{load}\) 与电压源连接之后，此时电阻 \(R\) 与电源内阻串联。根据分压公式，电压源的端电压为 \(V_T = V_S \frac{R_{load}}{R_{load} + r_s}\)，表明当负载电阻 \(R_{load}\) 远远大于电源内阻时（约 1000 倍以上），电源内阻 \(r_s\) 的影响较小可以忽略。但是当负载电阻 \(R_{load}\) 小于或者接近电源内阻时，就必须考虑到电源内阻的影响。

理想电流源

下面给出了电子学当中直流电流源的符号，它能够在任意时刻为负载提供一个恒定不变的电流 \(I_S\)，而不论负载电阻如何进行变化。这意味着为了保持电流源的电流恒定，理想电流源的端电压将会随着负载电阻的变化而变化。

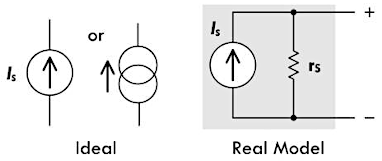
通常情况下，实际电流源都具有一个非常大的并联内阻，这个内阻可以使得电流源的端电流减小，减小量取决于电流源的电流值与端电压（或负载电阻的大小）。当电流源的两端开路时，电流源的电流 \(I_T\) 显然应该为零，但是如果在电流源两端接上负载电阻 \(R_{load}\)，与电流源的内阻 \(r_s\) 组成并联电阻电路，运用并联电阻分流公式，就可以得到其端电流 \(I_T = I_S \frac{r_s}{R_{load} + r_s}\)：

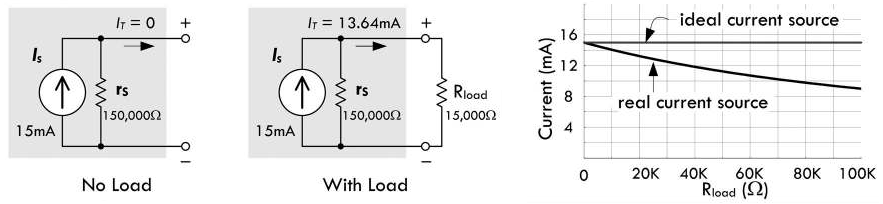
上式表明当负载电阻 \(R_{load}\) 小于电流源的内阻 \(r_s\) 时，流过内阻的电流将会非常小，通常可以忽略不计。但是当负载电阻 \(R_{load}\) 大于或者接近电流源内阻 \(r_s\) 的时候，计算时就必须考虑内阻 \(r_s\)。

电压源 & 电流源转换

一个电源既可以采用电流源表示，也可以采用电压源表示，本质上它们是相互等价的。两者之间进行相互转换时，首先保持电源内阻不变，然后应用欧姆定律将电压源的电压转换成电流源的电流：

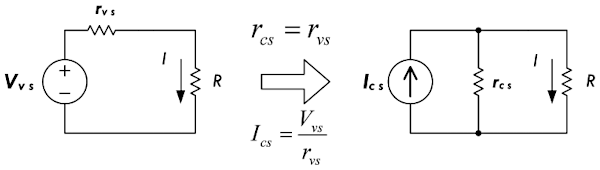
由于理想电流源的内阻是无穷大的，所以理想电流源的两端可以承受任意大小的电压（或者任意的负载电阻变化）。因而理想电流源可以采用一个具有极高电压 \(V\) 的电压源与一个较大的电阻 \(R\) 的串联组合，来近似的进行表示。如果负载电阻远远小于电阻 \(R\)，那么这个近似模型提供给任意负载的电流为 \(\frac{V}{R}\)。

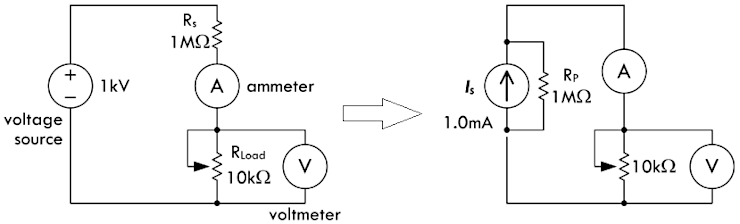
例如上图当中的电路由一个 1kV 的电压源与一个 1MΩ 的内阻串联组成，当负载电压保持在 \(0V \sim 10V\) 之间时（\(0<R_{load}<10kΩ\)），电路当中的电流将会维持在 1mA，而精度在 1％ 以内。实际上，即使负载电阻发生了变化，由于电压源的内阻远远大于负载电阻，电流也会保持不变 \(I = \frac{1000V}{1\ 000\ 000Ω + 100\ 000Ω}\)。由于 \(1\ 000\ 000Ω\) 的阻值较大，因而可以忽略负载电阻 \(R_{load}\)。

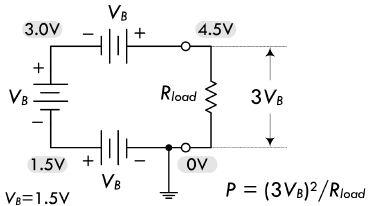
电池的串并联

电池串联之后会增大电压，输出电压等于每一节电池上的电压之和，输出电流等于每一节电池上经过的电流，输出总功率为 \(P = \frac{(n \times V_{battery})^2}{R_{load}}\)：

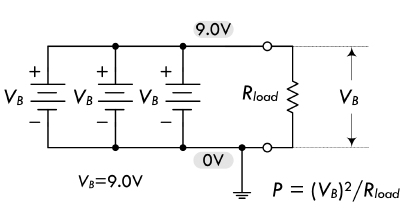
电池并联之后会增大电流，输出电压等于每一节电池两端的电压，输出电流等于每一节电池上经过的电流之和，输出总功率为 \(P = \frac{V_{battery}^2}{R_{load}}\)：

基尔霍夫定律

基尔霍夫定律给出了分析电路的最普遍的方法，该定律不仅适用于线性电路（含有电阻、电感、电容元件），同样也适用于非线性电路（含有二极管、三极管等元件），基尔霍夫定律主要包括有如下两个子定律：

1. 基尔霍夫电压定律（回路定律）：电路当中沿着任意一个回路的所有电压的代数和为零： \[ \sum_{close\ path} \Delta V = V_1 + V_2 + V_3 + ... + V_n \]
2. 基尔霍夫电流定律（节点定律）：流入一个节点的所有电流之和等于流出该节点的所有电流之和： \[ \sum \Delta I_{in} = \sum \Delta I_{out} \]

叠加原理

叠加原理适用于分析含有多个电源的线性电路，其内容是指线性电路任意一个支路上的电流，等于电路当中每一个电源单独作用时（其余电源置零，电压源短路，电流源开路）在该支路产生的电流之和。

例如下图左侧电路包含有两个电阻、一个电压源、一个电流源，应用叠加原理可以将其转换为后面两种形式：

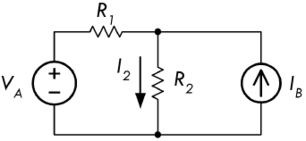
首先，把电流源置零，将电流源从电路里移除掉，也就是将电流源 \(I_B\) 的两个端子断开：

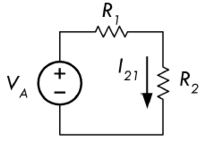
此时，上图当中流过电阻的电流，仅会由电压源 \(V_A\) 产生，其值等于电压 \(V_A\) 除以等效电阻：

\[ I_{21} = \frac{V_A}{R_1 + R_2} \]

然后，将电压源置零，直接通过导线让电压源两端短路，使得电路成为一个分流器：

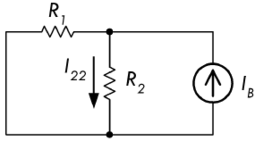
此时，电流源在电阻 \(R_2\) 两端产生的电流 \(I_{22}\) 等于：

\[ I_{22} = \frac{I_B R_1}{R_1 + R_2} \]

最后，运用叠加原理，将电流 \(I_{21}\) 与 \(I_{22}\) 相加，就可以得到支路 2 上所经过电流 \(I_2\) 的值：

\[ I_2 = I_{21} + I_{22} = \frac{V_A - I_B R_1}{R_1 + R_2} \]

注意：叠加原理是分析线性电路的一种重要方法，也是戴维南定理和诺顿定理成立的基础，这两者在电路分析当中相比叠加原理更为实用，实际电路分析当中较少直接应用到叠加原理。

戴维南定理

如果只关注电路当中两个端子之间所连接支路的参数，那么可以将这条支路从复杂电路当中断开，并且把剩余部分电路视为拥有两个端子的线性二端网络，然后采用一个电压源与一个电阻的串联支路来代替，这种电路分析方法就称为戴维南定理。

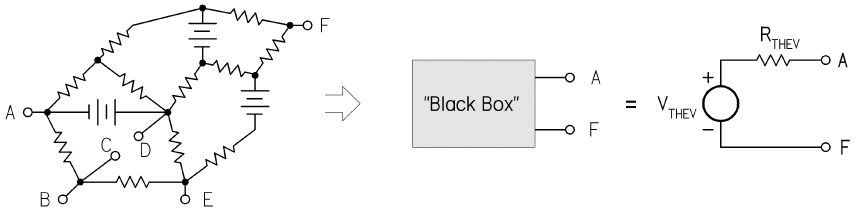
串联支路上的电压源称为戴维南等效电压 \(V_{THEV}\)，电阻称为戴维南等效电阻 \(R_{THEV}\)，而整个串联支路称为戴维南等效电路。运用这个简单的等效电路，再结合欧姆定律，就可以计算出其所连接电路上的负载电流 \(I = \frac{V_{THEV}}{R_{THEV} + R_{LOAD}}\)。

接下来，运用戴维南定理来求解下图左上角的分压电路：

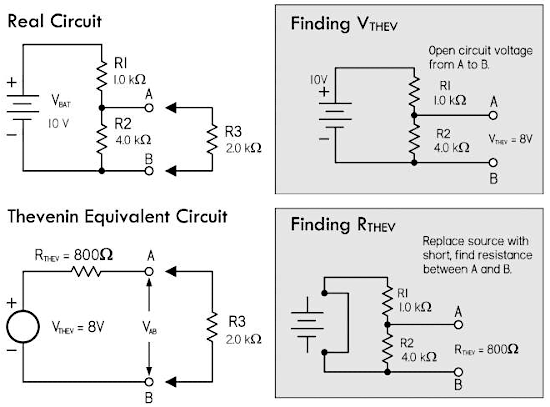
1. 首先，去掉负载 \(R_3\)，使得电路上的 A 与 B 两端断开，
2. 然后，应用欧姆定律或者分压公式求解出戴维南等效电压 \(V_{THEV}\)，也就是 A 与 B 两端的开路电压；
3. 接下来，计算 A 与 B 两端的戴维南等效电阻 \(R_{THEV}\)，把直流电源 \(V_{BAT}\) 短路，计算或者测量 A 与 B 两端的等效电阻 \(R_{THEV}\)，即电阻 \(R_1\) 与电阻 \(R_2\) 的并联等效电阻；
4. 最后，就可以得到使用 \(V_{THEV}\) 与 \(R_{THEV}\) 串联表示的戴维南等效电路，此时负载上的电压 \(V_3\) 与电流 \(I_3\) 分别为：

\[ \begin{cases} V_3 = \frac{R_3}{R_3 + R_{THEV}} \times V_{THEV} = \frac{2000Ω}{2800Ω} \times 8V = 5.7V \\ I_3 = \frac{V_{THEV}}{R_3 + R_{THEV})} = \frac{8V}{2800Ω} = 0.003A \end{cases} \]

诺顿定理

类似于戴维南定理，诺顿定理也是通过一个等效电路来代替复杂的二端网络，而不同之处在于诺顿等效电路是由一个电流源与一个电阻的并联所组成。其中，由于诺顿等效电阻的值与戴维南等效电阻恰好相等，因而只需要计算出电流源的诺顿等效电流 \(I_{NORTON}\) 即可。

接下来，对于前面采用戴维南定理分析的分压电路，这里改用诺顿定理来进行分析，其中诺顿电流 \(I_{NORTON}\) 就是节点 A 与 B 之间的短路电流：

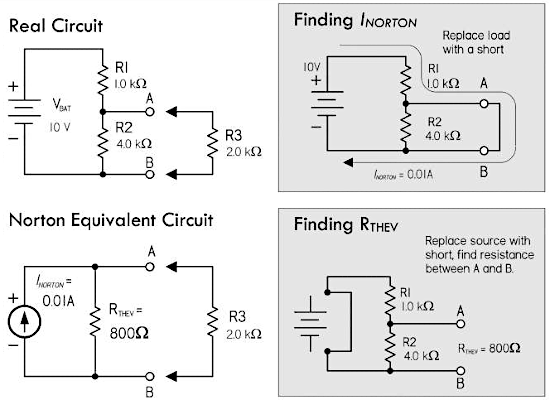
1. 首先，去掉负载 \(R_3\)，将 A 与 B 的两端短路，此时电阻 \(R_2\) 被短路没有电流经过，根据欧姆定律可以得到诺顿等效电流： \[ I_{NORTON} = \frac{V_{BAT}}{R_1} = \frac{10V}{1000Ω} = 0.01A \]
2. 然后，计算诺顿等效电阻，由于诺顿等效电阻与维南等效电阻相等，这里直接使用之前计算得到的戴维南等效电阻 \(R_{THEV} = 800Ω\)；
3. 最后，得到了诺顿等效电路，把 \(R_3\) 重新连接到等效电路，运用欧姆定律与分流公式就可以求解出经过 \(R_3\) 的电流：

\[ I_3 = \frac{R_{THEV}}{R_{THEV} + R_3} \times I_{NORTON} = \frac{800Ω}{2800Ω} \times 0.01A = 0.003A \]

注意：诺顿定理对应的是电流源，戴维南定理对应的是电压源，两者在本质上依然是叠加原理。诺顿等效电路与戴维南等效电路可以相互转换，它们转换之后的等效电阻都相同；戴维南等效电路中的等效电阻与等效电压源串联；而诺顿等效电路中的等效电阻与等效电流源并联；戴维南等效电路的电压等于诺顿等效电路空载时等效电阻上的电压。而诺顿等效电源的电流等于戴维南等效电源的短路电流。

动态电路理论

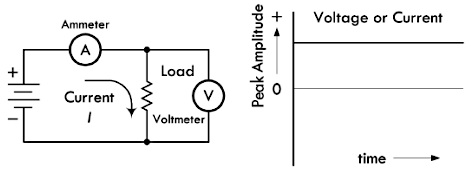
交流 & 直流

直流（DC）：电流或者电压的大小、方向都不会发生变化；

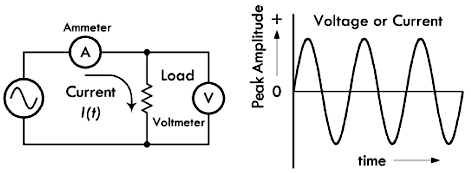
交流（AC）：电流或者电压的大小、方向均呈周期性变化；

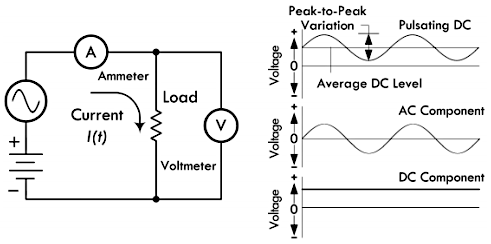
脉动直流（Pulse DC）：电流或者电压的大小变化，而方向不发生改变，可以将其视为交流与直流的叠加；

交流电的产生

交流发电机利用电磁感应原理可以产生正弦交流信号，下面示意图展示了一个由磁体和线圈构成的简单交流发电机，线圈放置在磁体的 N 极与 S 极之间，可以围绕轴心进行旋转。伴随线圈在磁场当中的旋转，通过线圈的磁通量不断发生变化，线圈当中的电荷由于受到磁场力而发生运动，从而在线圈两端形成感应电压。

通过线圈的磁通量 \(\varPhi\) 是线圈与磁场方向夹角 \(\theta\) 的函数，而感应电压是以 \(\omega\) 作为角频率（rad/s，弧度每秒）的正弦量。

交流与直流的叠加

下图是两个幅值相同，而且频率相近的交流信号，以及将它们串联之后得到的合成波形；注意两个交流信号的正向峰值点在合成之后，将会得到更高的峰值点，这就是所谓的拍现象，拍频率等于 \(f_2 - f_1 = 500Hz\)：

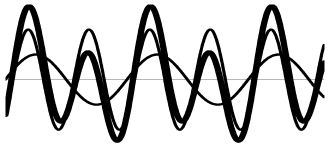
下图是两个频率与幅值相差较大的交流信号，以及使它们串联之后得到的合成波形，可以发现一个波驮载在另外一个波上面：

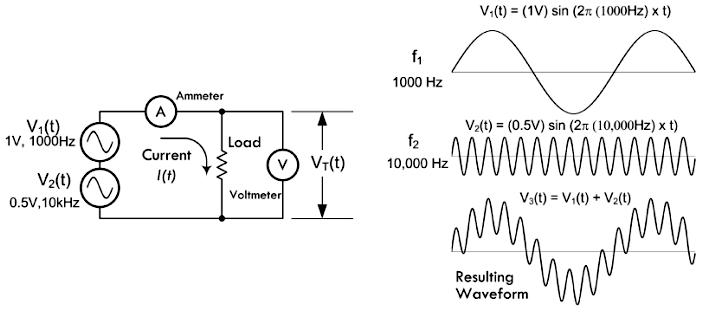
注意：把两个幅值与相位不同，但是频率相同的正弦波合成之后，得到的仍然是正弦波，这个特点在交流电路分析当中尤为重要。

其它波形

利用傅里叶变换，通过一系列正弦波的叠加，就可以获得任意的周期性波形：

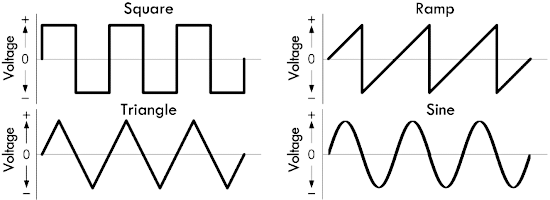
一个理想的正弦电压源，无论其负载如何，总是可以提供所需的电流并且维持两端的电压。而一个理想的正弦电流源，无论负载如何，都能够提供所需的电压并维持其输出电流。除此之外，还可以建立用于产生方波信号的时钟源。下图从左至右，分别展示了交流电压源、交流电流源、时钟源的符号：

交流信号三要素

交流电压或者电流信号的完整描述，需要使用幅值、频率、相位三要素。

幅值

下图展示了一个正弦电压或者电流的幅值，与一个逆时针旋转圆周的对应关系。电压、电流的幅值随着圆周上与 \(0°\) 线之间的夹角进行正弦变化，例如 \(\sin 90°\) 为 1，对应正半波的最大值；而 \(\sin 270°\) 为 -1，对应负半波的最大值；而 \(\sin 45°\) 为 0.707，对应着最大值的 0.707 倍：

频率 & 周期

持续转动的发电机可以产生正弦变化的电压或者电流，随着时间的不断推移，正弦波形也会不断的循环。在循环的波形上任意选取一点（例如正峰值位置）作为标记点，则每秒钟电流或者电压到达该标记点的次数，就称为交流电的频率。换而言之，频率表示的是电信号循环的速率，其单位为 赫兹 Hz。而每次循环所持续的时间称为周期，周期在数值上等于频率的倒数：

\[ \begin{cases} 频率f(Hz) = \frac{1}{周期T(s)} \implies f = \frac{1}{T} \\ 周期T(s) = \frac{1}{频率f(Hz)} \implies T = \frac{1}{f} \end{cases} \]

例如 60Hz 交变电流信号的周期为 \(T = \frac{1}{60Hz} = 0.0167S\)，而 2ns 周期交变电压信号的频率为 \(f = \frac{1}{2 \times 10^{-9}(s)} = 500MHz\)。

相位

绘制下图所示的电压、电流正弦曲线时，通常以 0° 作为计时起点，即信号正半周的起始点，而正向峰值则出现在 90° 位置。换而言之，相对于 0° 起始点，交流峰值所处的相位为 90°：

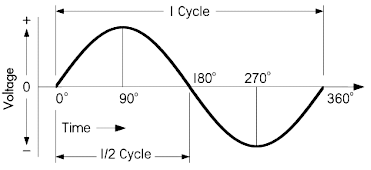
注意：一个交流信号的周期被划分为 360°，并以此作为时间与相位的计量单位。

相位可以用于比较频率相同的交流信号，例如下图所示的正弦波 A 先经过 0° 点，而正弦波 B 后经过 0° 点，两个波形之间存在着相位差。图中 B 滞后于 A 有 45°，或者说 A 超前于 B 有 45°。如果正弦波 A 和 B 出现在相同的电路当中，两者叠加之后合成的波形相位将会介于 A 与 B 的相位之间。而对于同频率的正弦波而言，叠加之后产生的合成波形频率相同，而幅值与相位将会发生改变：

注意：两个同频率正弦波起始点不同，它们之间的相位差可以采用弧度或角度进行度量，上图当中 B 的起始点比 A 滞后 1/8 周期，即 B 滞后于 A 有 45°。

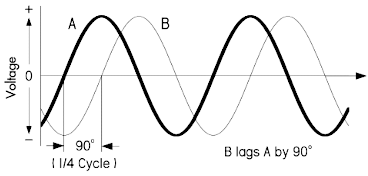
下图所示的是一种相位差的特殊情况，其中 B 滞后于 A 有 90°，也就是 B 恰好落后于 A 有 1/4 周期，即波形经过 0° 点时，另一个波形恰好到达峰值的位置：

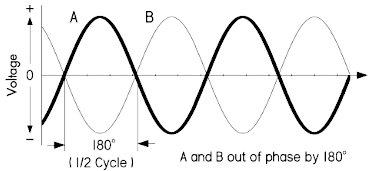
下图所示的是另外一种相位差的特殊情况，其中 A 与 B 相位差为 180°，因而当 A 波形为负的时候，B 波形为正，反之亦然。当在同一个电路当中，添加这样两个幅值相同的电压、电流信号时，将会导致它们相互抵消：

均方根有效值

如果向电阻的两端添加交流电压，则通过电阻的电流将会与交变电压的相位一致，根据交变电压与电阻的值，就可以基于欧姆定律计算出交变电流。例如信号发生器所产生正弦波的计算表达式为：

\[ V(t) = V_P \sin(2\pi \times f \times t) \]

上面等式当中的 \(V_P\) 是正弦电压峰值、\(f\) 为频率、\(t\) 为时间，利用欧姆定理与功率定理可以得到如下表达式：

\[ I(t) = \frac{V(t)}{R} = \frac{V_P}{R} \sin (2\pi \times f \times t) \]

将上述的 \(V(t)\) 与 \(I(t)\) 的波形，绘制在相同的坐标系当中。此时电流与电压的相位一致，即电流伴随着电压同时增大：

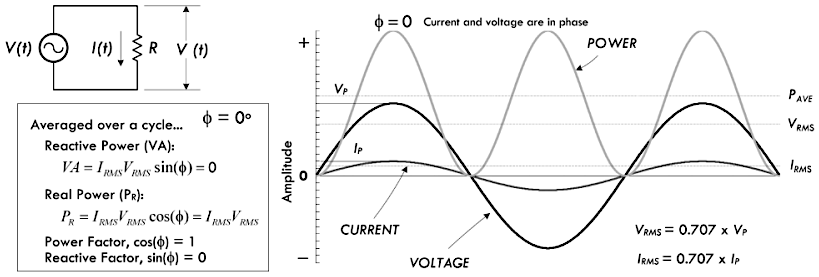
可以看到，当交流电源两端接入纯电阻负载时，电压与电流处于相同的相位。如果负载不是纯电阻负载（例如电容、电感），那么情况就将会完全不同（后续章节会进行介绍）。求解正弦信号下电阻所消耗的功率，可以将正弦电压的表达式直接代入欧姆定律，从而得到瞬时功率的表达式：

\[ P(t) = \frac{V(t)^2}{R} = \frac{V_P^2}{R} \sin(2 \pi \times f \times t) \]

从数学角度来看，电压、电流与功率的瞬时表达式并不复杂，只需要将具体时间 \(t = 1.3S\) 代入即可求解出实际值。但是仅获得某一具体时刻的电流、电压、功率意义不大，还必须知道计时的起点。实际应用当中，这些瞬时值很难获取。最有效的方法是采用平均值代替瞬时值，而且运用平均值计算有功功率损耗可以不涉及正弦函数。然而正弦波在一个周期当中的正、负波形会相互抵消，导致电压、电流的平均值为零。所以对于功率而言，正半波与负半波都在进行能量的传递。因而必须找到一个能够代替平均值的参数，而这个参数正是均方根值（RMS，Root Mean Square），这个值可以通过对交变电压、交变电流的瞬时值进行平方，然后获取其在一个周期当中的平均值，再对这个值进行开平方根来获得。

均方根值 RMS 也称为有效值，其实质是交流电压/电流与直流电压/电流所消耗热能的等效，即交流电的均方根值等于相同电阻元件消耗交/直流功率，产生同等热量时刻的值。根据上述原理，电阻在交流峰值时消耗的功率是直流时消耗功率的两倍，也就是说，平均交流功率是交流峰值功率的 \(\frac{1}{2}\)。

\[ 平均功率 P_{ave} = \frac{峰值功率 P_{peak}}{2} \]

假设正弦电压 \(V(t) = V_P \sin(2 \pi \times f \times t)\)、正弦电流 \(I(t) = I_P \sin(2 \pi \times f \times t)\)，则它们的 RMS 有效值表达式如下方程所示：

\[ \begin{cases} V_{RMS} = \sqrt{\frac{1}{T} \int_0^T V(t)^2 dt} = \frac{1}{\sqrt{2}} \times V_P = 0.707 \times V_P \\ I_{RMS} = \sqrt{\frac{1}{T} \int_0^T I(t)^2 dt} = \frac{1}{\sqrt{2}} \times I_P = 0.707 \times I_P \end{cases} \]

上述的推导过程表明，电压与电流的 RMS 值只与电压或者电流的峰值有关，而与时间和频率无关，通过简单的计算可以得到如下换算关系：

\[ \begin{cases} V_{RMS} = \frac{V_P}{\sqrt{2}} \approx \frac{V_P}{1.414} \approx 0.707 \times V_P \implies V_P \approx V_{RMS} \times 1.414 \\ I_{RMS} = \frac{I_P}{\sqrt{2}} \approx \frac{I_P}{1.414} \approx 0.707 \times I_P \implies I_P \approx I_{RMS} \times 1.414 \end{cases} \]

注意：美国家庭用电标准为 60Hz，1VAC，欧洲国家则普遍采用 50Hz，2VAC，单位 VAC 表示该电压值属于 RMS 均方根有效值。

把电压与电流的 RMS 有效值代人欧姆定律，就可以得到交流欧姆定律：

\[ V_{RMS} = I_{RMS} \times R \]

同样的，把电压与电流的 RMS 有效值代入功率定理，就可以得到交流功率定理（此处的功率是指有功功率）：

\[ P = I_{RMS} \times V_{RMS} = \frac{V_{RMS}^2}{R} = I_{RMS}^2 R \]

注意：上述公式只能应用于不包含电容与电感的纯电阻电路当中。

下面的表格，展示了上图电压与电流的均方根有效值、峰值、峰峰值、半波平均值之间的关系，掌握它们之间的换算关系尤为重要：

待转换类型	结果类型	换算因数
峰值	峰峰值	\(2\)
峰值	平均值 ★	\(\frac{2}{2 \pi}\) 或者 0.6366
峰值	有效值	\(\frac{1}{\sqrt{2}}\) 或者 0.7071
峰峰值	峰值	\(0.5\)
峰峰值	有效值	\(\frac{1}{2\sqrt{2}}\) 或者 0.35355
平均值 ★	峰值	\(\frac{\pi}{2}\) 或者 1.5708
平均值 ★	有效值	\(\frac{\pi}{2 \times \sqrt{2}}\) 或者 1.1107
有效值	峰值	\(\sqrt{2}\) 或者 1.4142
有效值	平均值 ★	\(\frac{2 \times \sqrt{2}}{\pi}\) 或者 0.9003
有效值	峰峰值	\(2 \times \sqrt{2}\) 或者 2.828

注意：上面表格当中标注有 ★ 符号的，表示的是半个周期内的平均值。

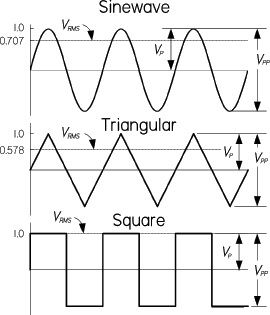
下面的表格，展示了上图所示正弦波、方波、三角波/锯齿波的半波平均值、峰值、峰峰值、有效值之间的换算关系：

波形	半波平均值	有效值	峰值	峰峰值
正弦波	1.00	1.11	1.567	3.14
... ...	0.90	1.00	1.414	2.828
... ...	0.637	0.707	1.00	2.00
... ...	0.318	0.354	0.50	1.00
方波	1.00	1.00	1.00	2.00
三角波或锯齿波	1.00	1.15	2.00	4.00
... ...	0.87	1.00	1.73	3.46
... ...	0.50	0.578	1.00	2.00
... ...	0.25	0.289	0.50	1.00

电容

在两块带有相反极性电荷的平行板之间，填充上绝缘介质，就可以制作成为一个平行板电容器：

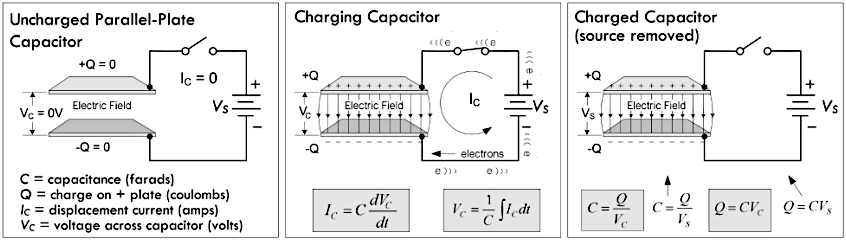
电容器是一种专门用于保存电荷，从而通过电场储存电能的元器件。如果移出电容器两极的电源，那么电容器自身的漏电流将会导致完全放电。或者采用一根导线连接电容器的两极，也可以中和两个极板上的异种电荷，从而达到快速放电的目的。

电容器当中存储的电荷量，与其两极之间电压的比值就称为电容，采用符号 \(C\) 进行表示：

\[ 电容 C = \frac{电荷 Q}{电压 V} \]

上述公式当中电容 \(C\) 的值总是取正值，单位为法拉，简写为 \(F\)，1 法拉等于一库仑每伏 \(1F = \frac{1C}{1V}\)。固定电容器、有极性电容器、可变电容器、微调电容器的符号(左侧)，以及实际电容器的等效模型(右侧)分别如下图所示：

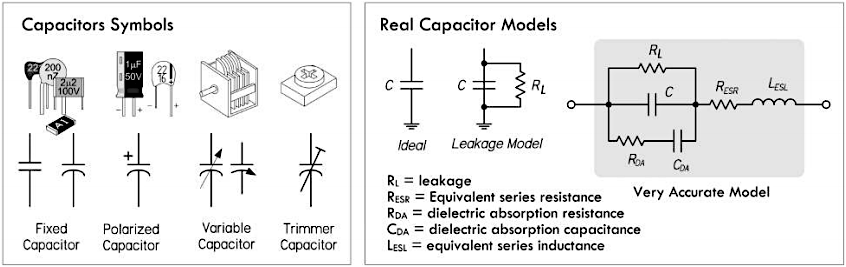
注意：电容器的取值范围比较宽泛，即可以在给定的电压之下存储不同的电荷量，也可以在给定电荷量的情况下维持不同的电压。因而选取合适的电容器，就能够控制电荷量或者电压。

电容值

电容器的容值与极板面积 \(A\)（单位为 \(m^2\)）、极板间距 \(d\)（单位为 \(m\)）、电介质的介电常数 \(\varepsilon\)（真空介电常数 \(\varepsilon_0 = 8.85 \times 10^{-12}\ C^2 /N \cdot m^2\)）有关。如果极板上的电压为 \(V\)，极板之间的电场强度 \(E = \frac{V}{d}\)，此时极板上必然携带有等量的异种电荷 \(Q\)：

\[ 电荷 Q = 介电常数 \varepsilon \times 极板面积 A \times 极板间电场强度 E = \frac{介电常数 \varepsilon \times 极板面积 A \times 两极电压 V}{极板间距 d} \]

上述方程当中的 \(\frac{\varepsilon A}{d}\) 部分，就是电容器 \(C\) 的容值计算公式：

\[ 电容值 C = \frac{介电常数\varepsilon \times 极板面积 A}{极板间距 d} \]

某一种介质的介电常数与真空的介电常数的比值，就称为该介质材料的相对介电常数 \(k\)：

\[ 相对介电常数 k = \frac{某物质介电常数 \varepsilon}{真空介电常数 \varepsilon_0} \]

将相对介电常数 \(k\) 的表达式，代入至上述的电容值 \(C\) 的表达式里，就可以得到下面的方程：

\[ 电容值 C = \frac{相对介电常数 k \times 真空介电常数 \varepsilon_0 \times 极板面积 A}{极板间距 d} = \frac{(8.85 \times 10^{-12}) \times 相对介电常数 k \times 极板面积 A}{极板间距 d} \]

相对介电常数的变化范围为 \(1.00059\)（一个标准大气压下的空气）到 \(10^5\)（某一些陶瓷材料），下面的表格展示了一些常见介质的相对介电常数：

通常情况下，电容器的极板数量不止两个，通过极板的交替层叠，就可以在较小空间内获得较大的容值，由 \(n\) 层极板构成的电容器容值表达式如下所示：

\[ 电容值 C = \frac{相对介电常数 k \times 真空介电常数 \varepsilon_0 \times 极板面积 A}{极板间距 d} \times (极板层数 n - 1) \]

注意：电容器的极板通常使用金属薄片制作而成，极板之间填充固态或者液态电介质（如云母、纸、聚丙烯、陶瓷）。其中，电解电容器的极板采用铝箔制成，极板之间填充的电介质为半液体状的化合物，电解电容器的容值通常较大，使用时需要区分其正负极性。极性的限制意味着电解电容不能直接应用于交流电路，但是可以应用于交流与直流叠加的电路当中，只要交流峰值电压不超过其最大直流工作电压（DCWV，Direct-Current Working Volts）即可，否则就会造成电介质击穿，在两个极板之间形成一道低阻的电流路径，导致电容器完全损坏。

理想电容/实际电容

理想电容器容值的微分形式可以记为 \(dQ = C \times dV\)，其中电容值 \(C\) 是一个不会随着电荷 \(Q\) 或者电压 \(V\) 变化的常量，而此时电流 \(I = \frac{dQ}{dt}\)，将其与电容的微分表达式联立之后，就可以得到经过电容器的电流 \(I_C\)：

\[ I_C = \frac{d 电荷量 Q}{d 时间 t} = \frac{d(电容值 C \times 电容电压 V_C)}{d 时间 t} = 电容值 C \times \frac{d 电容电压 V_C}{d 时间 t} \]

上面的方程表示在 \(dt\) 时间内，有大小为 \(C \times dVc\) 的微量电荷 \(dQ\) 流入右侧极板，同时在左侧极板上出现数量相同的电荷 \(dQ\)，即量值为 \(\frac{dQ}{dt} = \frac{C \times dV_C}{dt}\) 的电流进入了左侧极板。根据上述电容器经过电流 \(I_C\) 的微分方程，可以求解得到电容器上电压 \(V_C\) 的表达式：

\[ V_C = \frac{1}{C} \int I_C dt \]

上述方程针对的都是理想电容器，其所反映的各种特性，并不能直接应用于实际电容器，使用时应当加以鉴别和区分：

• 首先，如果在理想电容器两端施加直流电压，由于电压的变化率为 \(\frac{dV}{dt} = 0\)，则电容器的电流为 \(0\)，因而直流电路当中的电容器相当于开路。如果此时突然改变电压值，那么 \(\frac{dV}{dt} = \frac{9V}{0V} = \infty\)，此时电容器上的电流为无穷大 \(\infty\)，但是实际电路当中的电流不可能为无穷大。

  

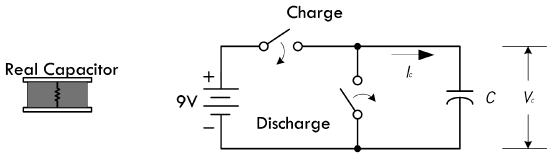
• 其次，电容器在直流状态下并没有电流经过，只有当其两端电压发生改变时，电容器才能够存储或者释放来自于电流的电荷。例如闭合上面电路当中的充电开关时，9V 电源会连接到电容器的两端，电容器中的电荷量立刻上升至最大值。然而对于实际电容器，由于其内电阻的存在，积累电荷需要耗费一定时间，使得位移电流不会为无穷大。而在电容器充电过程当中，电流会先突变至 \(\frac{V_{battery}}{R_{internal}}\) 而后迅速呈指数规律下降，与此同时电压会呈指数规律上升至与电源电压相等，下图是实际电容器在充电过程当中，电压与电流的变化曲线：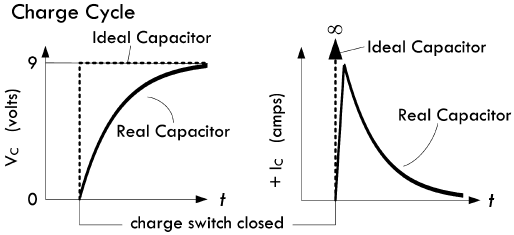

  

• 最后，当闭合放电开关之后，电容器的正负极板之间会形成一条导电路径，从而释放出与充电方向相反的电流，伴随着电荷的逐渐中和，电流从初始峰值 \(\frac{V_{battery}}{R_{internal}}\) 衰减，而电压则按照指数规律下降：

  

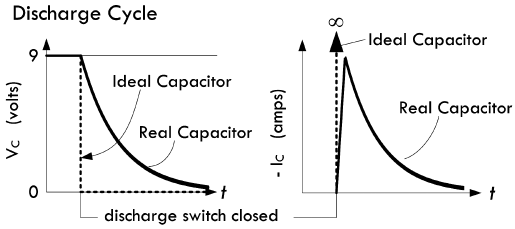
注意：由于实际电路当中经常存在电阻器元件，其电阻值远大于电容器的内阻，因而后者通常可以忽略，后续的RC 阻容电路将会更加详细的讨论这一点。

电容器存储的能量

虽然理想电容器不会消耗能量，但是实际电容器的内阻是会消耗能量的，不过该内阻值通常比较小，因而往往会忽略其造成的热损耗。

电容器当中的能量以电场的形式进行储存，将电容器的电流代入至功率表达式 \(P = IV\) 当中，再将结果代入功率的定义 \(P = \frac{dE}{dt}\) 里，对 \(E\) 进行积分，就可以获得电容器上面存储的能量 \(E_{cap}\)：

\[ E_{cap} = \int VIdt = \int VC \frac{dV}{dt} = \int CVdV = \frac{1}{2} CV^2 \]

例如在 \(1000 \mu F\) 的电容器两端添加 5V 的电压，那么该电容器里面存储的能量 \(E_{cap}\) 等于：

\[ E_{cap} = \frac{1}{2} CV^2 = \frac{1}{2} \times (1000 \times 10^{-6}F) \times (5V)^2 = 0.0125 J \]

RC 时间常数

首先，将电容器连接到直流电压源的两端，使其在一瞬间完成充电。然后，再把充满电的电容器两端进行短接，使其在一瞬间完成放电。基于这个过程，如果在该电路里加入一个电阻器，那么其充放电速率将会遵循下图所示的指数规律：

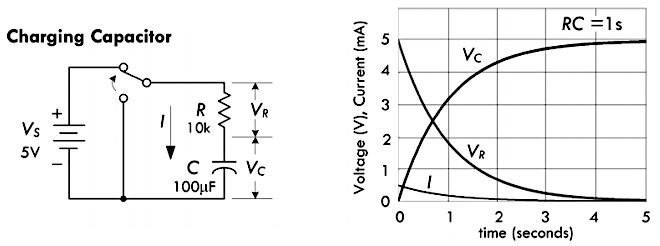
上图左侧 RC 充电电路当中的电阻 \(R= 10kΩ\)，而电容 \(C = 100 \mu F\)，其波形图如右侧所示。此时电路当中的电阻电压 \(V_R\)、电容电压 \(V_C\)、电流 \(I\) 之间的关系如下面方程所示：

\[ \begin{aligned} I = \frac{V_S}{R} e^{-\frac{t}{RC}} &\implies \frac{t}{RC} = - \ln \bigg(\frac{IR}{V_S} \bigg) \\ V_R = IR = V_S \cdot e^{-\frac{t}{RC}} &\implies \frac{t}{RC} = - \ln \bigg(\frac{V_R}{V_S} \bigg) \\ V_C = \frac{1}{C} \int Idt = V_S(1 - e^{-\frac{t}{RC}}) &\implies \frac{t}{RC} = -\ln \bigg( \frac{V_S - V_C}{V_S} \bigg) \end{aligned} \]

上述方程当中电流 \(I\) 的单位为安培，电压源 \(V_S\) 的单位为伏特，电阻 \(R\) 的单位为欧姆，电容 \(C\) 的单位为法拉，接入电压源后的时间 \(t\) 单位为秒，除此以外自然常数 \(e \approx 2.718\)。

通常以小写字母 \(\tau = t = RC\) 来表示电路的时间常数（单位为秒），表示的是 RC 电路当中，电容器通过电阻从初始的 0 电压，充电至最大电压的 63.2% 所需要的时间；或者是通过同一个电阻，将电容放电至其初始电压 36.8% 所需要的时间。

1. 经过 1 个时间常数 \(t = RC = \tau\) 以后，电容器上的充电电压达到电源电压的 63.2%；
2. 经过 2 个时间常数 \(t = 2RC = 2\tau\) 以后，电容器上的电压达到电源电压的 86.5%；
3. 经过 3 个时间常数 \(t = 3RC = 3\tau\) 以后，电容器上的电压达到电源电压的 95%；
4. 以此类推，在 5 个时间常数以后，电容电压为电源电压的 99.24%，可以认为已经充电完毕；

下图右侧 RC 放充电电路当中的电阻 \(R = 3kΩ\)，而电容 \(C = 0.1 \mu F\)，其波形图如右侧所示：

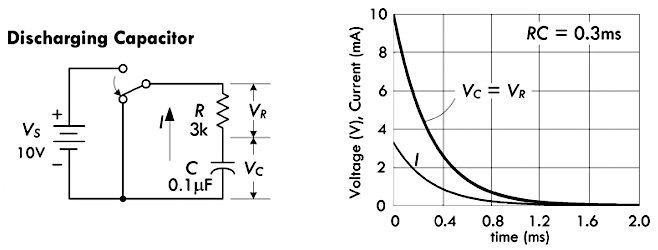
此时电路当中的电阻电压 \(V_R\)、电容电压 \(V_C\)、电流 \(I\) 之间的关系如下面方程所示：

\[ \begin{aligned} I = \frac{V_S}{R} e^{-\frac{t}{RC}} &\implies \frac{t}{RC} = - \ln \bigg(\frac{IR}{V_S} \bigg) \\ V_R = IR = V_S \cdot e^{-\frac{t}{RC}} &\implies \frac{t}{RC} = - \ln \bigg(\frac{V_R}{V_S} \bigg) \\ V_C = \frac{1}{C} \int_0 Idt = V_S \cdot e^{-\frac{t}{RC}} &\implies \frac{t}{RC} = -\ln \bigg( \frac{V_C}{V_S} \bigg) \end{aligned} \]

RC 电路当中，电容器的放电过程，正好与其充电过程完全相反：

1. 经过 1 个时间常数 \(t = 1\tau\) 以后，电容电压下降 63.2%，为电源电压的 37．8%；
2. 经过 5 个时间常数 \(t = 5\tau\) 以后，电容电压下降 99.24%，为电源电压的 0.76%，可以认为此时已放电完毕；

寄生电容

电容效应并不只存在于电容器的内部，不同电位的表面相互靠近时也会产生电场，从而也存在电容效应，称为寄生电容。这种效应会对电路造成不必要的干扰，因而必须采取措施降低其影响：

• 让电容器的引脚尽可能的短；
• 对相同电位的元件进行分组避免形成电容耦合；

高阻抗电路当中，由于容性电抗占据电路阻抗的比例较大，因而寄生电容造成的影响也会更大。除此之外，由于寄生电容往往与电路形成并联，当信号频率较高时，就会造成正常信号被旁路的问题。

电容的并联

当多个电容器进行并联时，总电容 \(C_{total}\) 等于各个并联电容的容值之和，其计算方式类似于串联电阻：

\[ C_{total} = C_1 + C_2 + C_3 + C_4 + ... C_n \]

注意：可以将电容器的并联，直观的视为增大了电容器极板的面积。

对于下面电路的上半部分结点，运用基尔霍夫电流定理可以得到 \(I_{total} = I_1 + I_2 + I_3 + ... + I_n\)：

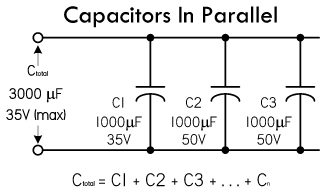
由于电容 \(C_1\) 与 \(C_2\) 两端的电压均为 \(V\)，将其代入上面的基尔霍夫电流方程，化简之后结果中的括号部分，就是并联等效电容的计算公式：

\[ I = C_1 \frac{dV}{dt} + C_2 \frac{dV}{dt} + C_3 \frac{dV}{dt} + ... + C_n \frac{dV}{dt} = (C_1 + C_2 + C_3 + ... + C_n) \frac{dV}{dt} \]

注意：并联电容器两端的安全电压，主要受限于额定电压最低的那一个电容。

电容的串联

当多个电容器串联在一起的时候，总电容 \(C_{total}\) 的倒数等于每一个串联电容器容值的倒数之和，其计算方式类似于并联电阻：

\[ \frac{1}{C_{total}} = \frac{1}{C_1} + \frac{1}{C_2} + \frac{1}{C_3} + ... + \frac{1}{C_n} \]

串联之后的总电容将会降低，并且小于容值最小的那个电容；每一个串联电容器两端的电压，等于输入电压 \(V_{IN}\) 的分数 \(V_{IN} \cdot (\frac{C_{total}}{C_2})\)，许多电路就利用到了电容器的这种分压特性：

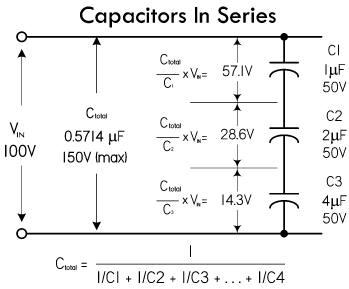
由于每一个串联电容器上的电流 \(I\) 相等，根据基尔霍夫电压定理得到下面的方程，该方程最后结果的括号部分，就是串联等效电容的计算公式：

\[ V = \frac{1}{C_1} \int Idt + \frac{1}{C_2} \int Idt + \frac{1}{C_3} \int Idt + ... + \frac{1}{C_n} \int Idt = \bigg ( \frac{1}{C_1} + \frac{1}{C_2} + \frac{1}{C_3} + ... + \frac{1}{C_n} \bigg ) \int Idt \]

注意：每一个串联电容器两端的电压，都不得超过其额定电压，必要时可以借助分压电阻来避免电容器损坏。

电容与交流信号

交流电路当中的电容器，可以允许或者限制特定频率的电流通过。下图所示的就是在交流信号下，电容器的电压、电流、功率关系曲线：

上图当中正弦电压的最大值为 100V，在 0 ~ A 这段时间里，外加电压从 0V 上升至 38V，此时电容器也会被充电至 38V；而在 A ~ B 阶段，外加电压上升至 71V，电容器电压也随之提高了 33V，由于 A ~ B 阶段电容器的电压增量相比 0 ~ A 阶段要小，因而电容器的电荷增量也要比 0 ~ A 阶段更少；到了 B ~ C 阶段，外加电压从 71V 上升至 92V，电容器电压随之提高了 21V，电压增量继续减小；继续到 C ~ D 阶段，外加电压只增加了 8V，电压增量进一步减小。

如果把前 \(\frac{1}{4}\) 周期分割为多个时间段，就会发现电容器的充电电流波形与外加电压一样为正弦波，周期起始点的电流为最大值，当电压达到最大值时电流变为零，表明在电压与电流之间存在着 -90° 相位差。第二个 \(\frac{1}{4}\) 周期，也就是 D ~ H 这段时间，外加电压降低，电容器将电荷释放回电路，并且电流方向与充电电压的方向相反；第三、四个 \(\frac{1}{4}\) 周期，将会分别重复第一、二个 \(\frac{1}{4}\) 周期的过程，不同之处在于外加电压的极性相反，电流也会发生相应的改变。换而言之，电容器的充放电过程产生了交变电流。

注意：通过电容器的的电流超前于电压有 90° 度。

容抗

电容器上面的电荷量正比于电容与外加电压 \(Q = CV\)，一个交流电路当中，电荷在电路当中进行周期性的往返运动，电荷/电流的运动速度与电压、电容、频率呈正比关系。将电容与频率相乘，就可以得到一个类似于电阻的参数容抗 \(X_C\)，其单位与电阻一样为欧姆 Ω：

\[ 容抗 X_C = \frac{1}{2 \pi \times 频率 f \times 电容 C} = \frac{1}{角频率 \omega \times 电容 C} \]

上面公式当中，容抗 \(X_C\) 的单位为欧姆 Ω，频率 \(f\) 的单位为赫兹 Hz，电容 \(C\) 的单位为法拉 F，而圆周率 \(\pi\) 约等于 3.1416，而 \(2 \pi f\) 通常使用角频率 \(\omega\) 进行代替。

当频率 \(f\) 为无穷大时，容抗 \(X_C\) 等于零，即高频时电容器相当于短路，可以认为电容器具有高通特性。而当频率 \(f\) 等于零时，容抗 \(X_C\) 趋于无穷大，电容器相当于断路，可以认为电容器具有抑制低频信号的特性。

注意：虽然容抗 \(X_C\) 的单位为欧姆，但是容抗并不会消耗电能。在 \(\frac{1}{4}\) 周期内存储在电容器的电能，会在下一个 \(\frac{1}{4}\) 周期释放回电路，即一个周期当中的平均功率为零。

下图展示了各种理想电容器的容抗与频率之间的关系，可以看出两者呈现反比关系：

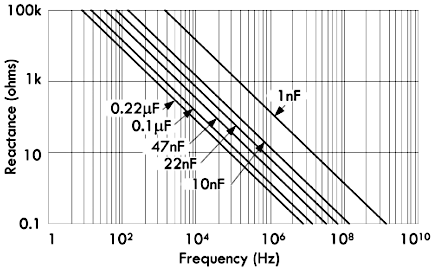
实际电容器需要考虑到电容内阻以及电感效应，其容抗与频率的关系如下图所示，图中曲线的最低点表示电容器的谐振点，该频率点下电容器的电容与电感效应相互抵消，因而只剩下内阻，这个点的频率就被称为谐振频率：

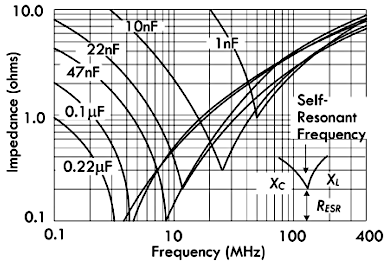
上图当中，实际电容器的阻抗，首先会随着频率的增大而减小，然后又会随着频率的增大而增大。由于实际电路当中寄生效应的存在，电容器的曲线与上图描绘的曲线可能并不完全一致。

电容分压电路

电容器分压电路通常只用于交流电路当中（由于电容器会隔断直流电压，所以其构成的分压电路不能工作在直流状态），电容器分压电路的交流输出电压 \(V_{out}\) 计算公式与电阻分压电路不同，其分子是串联电容 \(C_1\) 而非 \(C_2\)：

注意：电容器分压电路的输出电压与输入电压的频率无关。

品质因数 Q

对于电容、电感等储能元件，可以通过品质因数 Q 来区别其性能优劣。这类元件的 Q 值等于元件存储的能量（即储能相关的参数电抗）与其内部消耗的能量（即耗能相关的参数电阻）之比：

\[ 品质因数 Q = \frac{电抗 X}{电阻 R} \]

品质因数 Q 没有单位，电容器的电抗 \(X\) 就等于其容抗 \(X_C\)，而电感器的电抗 \(X\) 同样等于其感抗 \(X_L\)，电阻 \(R\) 表示的是元件中与能量消耗相关的全部内阻。

注意：电容器的 Q 值通常都比较高，例如陶瓷电容器和云母电容器的 Q 值可以达到 1200 以上；而微型可调陶瓷电容器的 Q 值比较小，某些应用场合下可以忽略；而微波电容器的 Q 值在 10GHz 以上工作频率不会超过 10。

电感

电子学当中的三个基本元件分别是电阻、电容、电感。其中，电容器以电场的形式存储电能，而电感器则是以磁场的形式储存电能。现代物理将电场与磁场结合起来形成了场论，称为电磁学。

电磁感应

磁场可以使得导体内部的电子受力，并且沿着某一个方向移动形成电流，其作用效果类似于电路里的电动势（EMF，Electromotive Force），通常称为感应电动势，根据法拉第电磁感应定律，电路当中的感应电动势与磁通变化率成正比：

\[ 感应电动势 EMF = - \frac{d\ 磁通量 \varPhi_M}{d\ 时间 t} \]

上面等式当中的 \(\varPhi_M\) 是穿过闭合回路的磁通量，其值等于磁场强度 \(B\) 与面积 \(A\) 点积的积分：

\[ 磁通量 \varPhi_M = \int 磁场强度 B \cdot d\ 面积 A \]

可以看到，在电路当中产生感应电动势的途径，主要存在如下三种：

1. 磁场强度 \(B\) 随着时间 \(t\) 进行变化；
2. 电路的回路面积 \(A\) 随时间 \(t\) 进行变化；
3. 磁场强度 \(B\) 与回路面积 \(A\) 的法线角度随时间 \(t\) 变化；

电感器

自感是指通过闭合线圈的电流发生了变化，致使线圈本身产生感应电动势的现象。电感器就是一种基于自感原理的电子元器件。其通常具有环状结构，内部可以产生较大的磁通。当电流变化较大时，也可以承受住较大的自感电压。

下图分别展示了空芯电感器、磁芯电感器、可调电感器、铁氧体磁环的电路符号：

• 空芯电感器：射频场景应用较多，可以避免由于内部磁滞与涡流引起的损耗；
• 磁芯电感器：产生的磁场强度比空心电感器更大，通过较少线圈匝数就可以实现较大的电感值；
• 可调电感器：通过改变磁芯长度，或者沿着线圈安置滑块，以及在磁芯中放置能够削弱磁芯磁通量的金属小块等方式，来实现电感值的可调；
• 铁氧体磁环：没有缠绕线圈，使用时直接将导线穿过磁环；

电感器工作原理

当电感器两端电压值增大时，电路当中的电流随之增大，通过螺旋线圈的磁通量也将会增大。增大的磁通量会对自由电子产生反向的作用力，这个作用力就是与初始电压方向相反的感应电动势，称为反向感应 EMF。

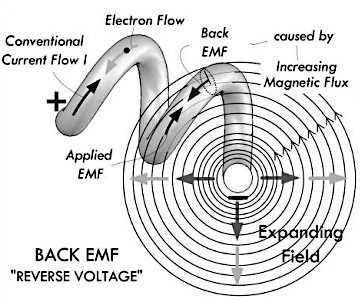
而当电感器两端电压值降低时，电路当中的电流随之减小，通过螺旋线圈的磁通量也将会减小。减小的磁通量会对自由电子产生同向的作用力，这个作用力就是与初始电压方向相同的感应电动势，称为同向感应 EMF。

电感的充磁

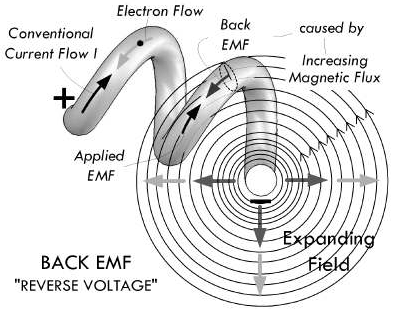
电感的充磁是指电源提供的能量传递到电感磁场的过程，例如下图所示电路当中，将开关由 B 拔向 A 时，电感上的电压发生改变，产生一个突然增大的电流，此时电感的磁场从零开始快速增大，这个过程就称为电感的充磁。

根据法拉第电磁感应定律，随着电感线圈磁通量的增大，线圈内的自由电子受到一个与电源电压方向相反的作用力（反向感应 EMF）:

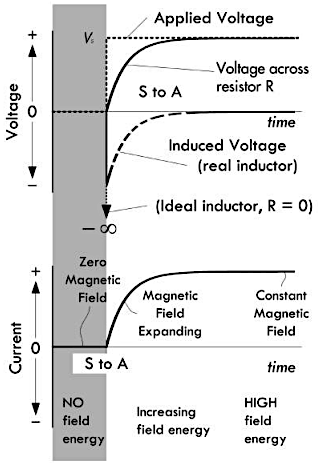
反向感应电动势的作用结果是在电流增大时，电感产生的阻力也在增大。一段时间之后，电路里的电流不再上升，磁场强度也停止变化，通过线圈的磁通量也不再发生变化，此时反向感应电动势消失，电感呈现为直接导通的状态。下面示意图的上半部分是电源电压与感应电压的关系曲线，而下半部分则是经过电感的电流曲线 \(I = \frac{V_s}{R}(1 - e^{-t/(L/R)})\)：

电感的去磁

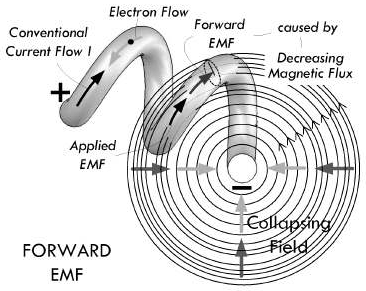
电感的去磁就是将电感中的磁场能量释放回电路，从而转换为电能的过程。将开关由 A 拔向 B 时，电感上的电压发生改变，使得电流趋于零，此时电感的磁场强度骤然减小，这个过程就称为电感的去磁。

去磁过程当中，电感会力图阻止磁场的减小，根据法拉第电磁感应定律，通过线圈的磁通量减小，线圈内的自由电子会受到与开关拔动之前的电源电压同向的作用力（同向感应 EMF）。因而电感会在电流降低的过程当中，充当电源的角色为电路提供电流，其所提供的能量来自于磁场的变化：

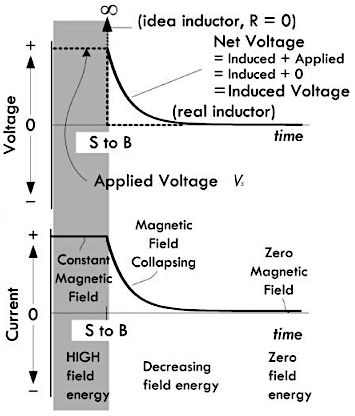
下面示意图的上半部分同样是电源电压与感应电压的关系曲线，而下半部分依然是经过电感的电流曲线 \(I = \frac{V_s}{R}(e^{-t/(L/R)})\)：

电感系数

电感的感应电压 \(V_L\)（感应电动势）与电流 \(I_L\) 的关系可以采用下面的方程来进行表示：

\[ 感应电压 V_L = \frac{d\ 电流 I_L}{d\ 时间 t} \]

分别对上述方程的左右两侧进行积分，就可以求解得到电流 \(I_L\) 的表达式：

\[ 电流 I_L = \frac{1}{电感系数 L} \int 感应电压\ V_L\ \cdot d\ 时间\ t \]

该表达式中的 \(L\) 称为电感系数，其大小与电感的物理特性相关，例如线圈的形状与匝数、磁芯的材料与结构等。

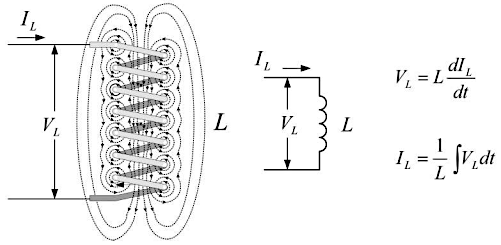
注意：理想电感两端的电压是感应电压 \(V_L\)，当稳态直流通过电感时 \(V_L = 0\)，此时电感相当于短路。

电感系数的单位为亨利 H，1H 等于当电流变化率为 1A/s 时 1V 的感应电压，即 \(1 H = \frac{1V}{1 A/s}\)。电子元件厂商生产的电感器，其典型电感系数范围在 \(0.1nH \sim 50H\) 之间，除了亨利 H 这个单位之外，电感系数的常用单位还有纳亨 nH、微亨 μH、毫亨 mH：

\[ 1 H = 10^3 mH = 10^6 μH = 10^9 nH \]

电感系数也可以根据其物理原理来进行定义，即任意时刻的电感系数等于磁通链 \(N \varPhi_M\) 与电流 \(I\) 的比值：

\[ 电感 L = \frac{磁通链 N \varPhi_M}{电流 I} \]

对于下图所示的空心螺线管，当流过线圈的电流为 \(I\)，应用安培定律就可以计算出其磁通量 \(\varPhi_M\)：

\[ \varPhi_M = B \cdot A = \bigg( \frac{\mu_0 NI}{l} \bigg) \cdot A = \mu_0 A n_{unit} I \]

上述计算过程当中，\(n_{unit}\) 为线圈单位长度的匝数 \(n_{unit} = \frac{N}{l}\)，其中 \(N\) 为总匝数，\(l\) 为线圈长度，\(A\) 为横截面积，\(\mu\) 为线圈内芯的磁导率。除金属铁以及铁氧体之外，大多数材料的磁导率都近似为空气的磁导率 \(\mu_0 = 4 \pi \times 10^{-7}\ T\cdot m/A^2\)。

根据法拉第电磁感应定律，每匝线圈上面都存在着感应电压，因而总感应电压 \(V_L\) 为磁通量 \(\varPhi_M\) 变化率的 n 倍，这里的 n 表示的是线圈匝数：

\[ V_L = N \times \frac{d \varPhi_M}{dt} = \frac{\mu N^2 A}{l} \times \frac{dI}{dt} \]

上式当中的 \(\frac{\mu N^2 A}{l}\) 部分就是电感线圈的电感系数 \(L_{sol} = \frac{\mu N^2 A}{l}\)，其值伴随着线圈总匝数 \(N\) 的平方进行变化，如果匝数增加 1 倍，那么电感系数将会增加 4 倍；如果让线圈的电感系数增加 1 倍，则匝数应为线圈原有匝数的 \(\sqrt{2}\) 或者 1.414倍。

电感器上的能量

类似于之前介绍的理想电容器，理想电感器同样不消耗能量，而是将能量存储在磁场当中，当磁场减小的时候，又会将能量释放回电路。利用功率定理 \(P = IV\)，结合功率的定义 \(P = \frac{dW}{dt}\) 和电感方程 \(V = \frac{LdI}{dt}\)，并使用电感的储能 \(E_L\) 代替功 \(W\) 就可以获得如下的推导过程：

\[ 储能 E_L = \int P dt = \int IV dt = \int IL \frac{dI}{dt} dt = \int LI dt = \frac{1}{2} LI^2 \]

上面等式当中，能量 \(E_L\) 的单位为焦耳 J，电流 I 的单位为安培 A，电感 L 的单位为亨利H。

注意：实际电感器只会有少部分的能量被其内电阻以热量的形式损耗。

电感器结构

电感线圈通常绕制在磁性材料上面，例如叠片式铁芯、铁氧体混合材料，磁芯可以增大线圈的磁通密度，进而提高电感系数。

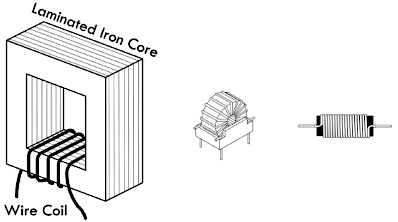
注意：磁芯线圈产生磁通密度与空芯线圈产生磁通密度的比值，称为磁芯材料的相对磁导率 \(\mu_R = \frac{\mu}{\mu_0}\)。

如果磁芯材料是导体（相比于钢制材料，铁氧体材料电阻率更大），那么在磁场发生变化时，磁芯材料内部就会产生下图所示的涡流效应：

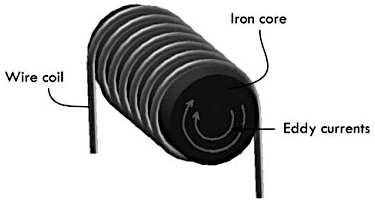
当流过线圈的电流增大时，通过磁芯的磁通量就会发生变化，磁芯材料当中就会感应到环路电流，出现类似于电阻的热损耗，这种现象就称为涡流效应（低阻抗率材料的涡流损耗较大）。为了避免这种情况的发生，可以将涂有绝缘漆的导体薄片，层叠在一起构成磁芯，从而降低磁通变化所引起的涡流效应。

除了涡流效应之外，使用钢制材料的另一个问题在于其磁导率会随着磁场强度、电流、温度的变化而发生变化。当磁场强度足够大时，钢制磁芯将会发生饱和，其相对磁导率会降低至约等于 1 的水平。钢制磁芯的磁场与线圈当中电流的变化过程有关，这种剩磁特性在电感器当中，会造成额外的损耗，这种损耗被称为磁滞损耗。为了避免这种情况的出现，必须让磁芯式电感器工作于非饱和状态。通过降低工作电流、使用较大磁芯、改变线圈匝数、使用低磁导率的磁芯或者带有空气间隙的磁芯，都可以完成这个目标。

注意：当涡流与磁滞造成的损耗较大时，电感的特性更加类似于一个电阻器。除此之外，由于电感线圈存在着匝间电容，因而在某些情况下，还会呈现出类似于电容器的特性。

实际电感/理想电感

下面公式当中的 \(\frac{d I_L}{dt}\) 表示的是通过电感的电流相对于时间的变化率，如果通过电感的电流不变，那么电感两端就不会存在着电压。如果一段时间内，流过电感的电流是直流，那么 \(\frac{d I_L}{dt} = V_L = 0\)，因而直流条件下电感相当于短路。

\[ V_L = L \times \frac{d I_L}{dt} \]

如果经过电感的电流 \(I_L\) 随着时间 \(t\) 发生变化，那么 \(\frac{d I_L}{dt} \neq 0\)，此时电感两端就会出现感应电压。

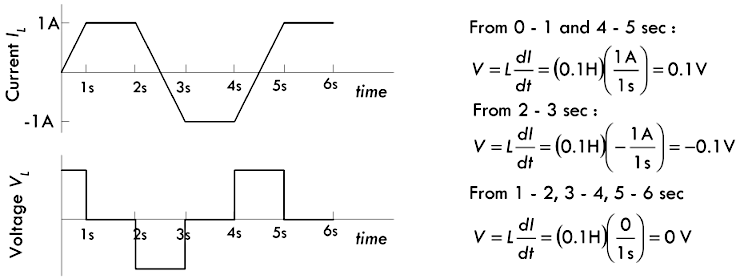
1. 在 0 ~ 1 秒 这段时间内，电流的变化率为 \(\frac{d I_L}{dt} = 1 A/s\)，如果电感系数 \(L = 0.1H\)，那么这段时间产生的感应电压 \(V = 0.1 H \times 1 A/s = 0.1V\)；
2. 在 1 ~ 2 秒 这段时间内，电流保持恒定 \(\frac{d I_L}{dt} = 0 A/s\)，因而这段时间产生的感应电压为 \(V = 0.1 H \times 0 A/s = 0\)；
3. 在 2 ~ 3 秒 这段时间内，电流变化率为 \(\frac{d I_L}{dt} = -1 A/s\)，则这段时间产生的感应电压 \(V = 0.1 H \times -1 A/s = -0.1V\)；

假设一个理想电感 \(L\) 与 10V 的电源 \(V_s\) 通过一个开关进行连接：

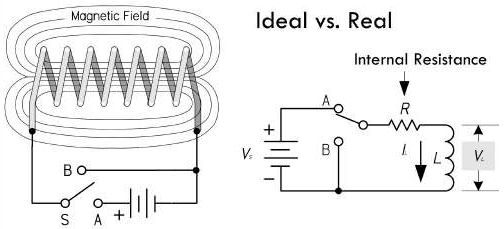
当开关闭合的一瞬间，根据电感方程 \(V_L = L \times \frac{d I_L}{dt}\)，可以推断出 \(\frac{d I}{dt}\) 将会趋于无穷大，这就意味着感应电压的上升情况正比于电源电压，电路当中没有电流通过，反向电压为无穷大（下图上半部分）。同样的，如果把开关打开，则会产生一个无穷大的同向电压（下图下半部分）。

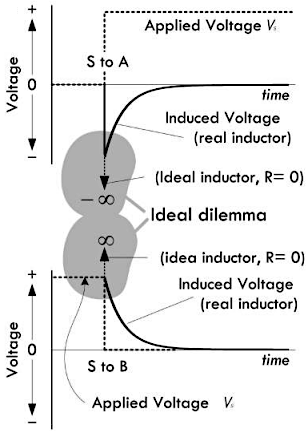
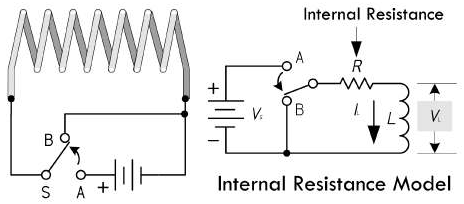
但是在现实世界当中，不可能出现无穷大的电压值，因为实际电感器上总是存在着内阻以及内部电容，所以下面的实际电感模型模型当中，就包含进了内阻与电容的参数。

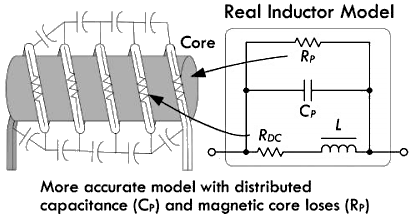
电感方程之所以没有直接包含一个内阻项的原因，在于电感系数 \(L\) 是一个独立的参数，其大小只会与磁场能量的变化相关，而不会与线圈的电阻与电容损耗相关。分析诸如 RL 和 RLC 这类更为复杂的电路时，在电路当中使用分散的电阻，就可以防止电感方程出现奇异解。

当需要进行精确的分析时，如果必须考虑到电感的内阻，那么可以使用理想电感和电阻 \(R_{DC}\) 的串联来作为实际电感模型，这个串联的 \(R_{DC}\) 称为电感的直流电阻。如果需要进行更为精确的分析（例如高频电路场景），那就必须同时考虑到内阻和电容效应，此时可以再在理想电感上面并联一个电阻 \(R_P\) 和一个电容 \(C_P\)，正如上面的示意图所展示的那样。

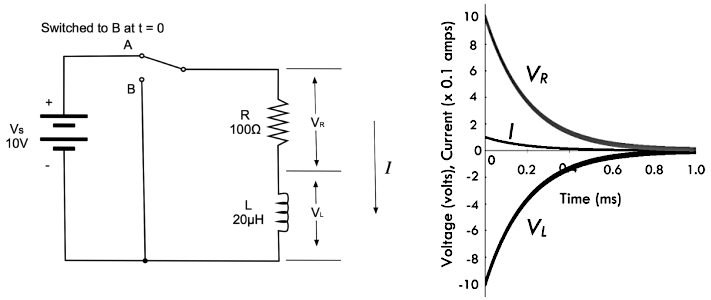
LR 充电电路

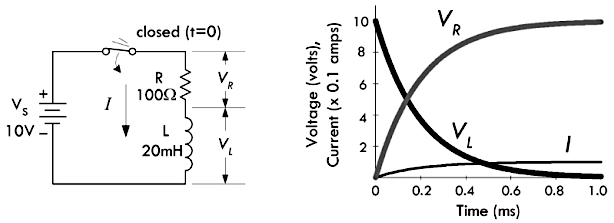
下面左图所示的 RL 电路由电阻与电感串联组成，电阻会控制输入电感磁场的能量变化速率，而在磁场减小的时候，电阻也会控制能量释放回电路的速率。假设下图左侧电路的电阻 \(R = 100Ω\)，而电感 \(L = 20mH\)，开关闭合的瞬间 \(t = 0\)，则其电压与电流的响应曲线如下面右图所示：

上述 RL 充电电路的电流与电压方程如下所示，其中 \(\tau = \frac{L}{R}\) 为时间常数，而常数 e = 2.718。除此之外，电流的单位为安培、电源电压 \(V_S\) 与电阻电压 \(V_R\) 以及电感电压 \(V_L\) 的单位都为伏特、电阻 \(R\) 的单位为欧姆、电感系数 \(L\) 的单位为亨利、而 \(t\) 表示接入电源之后的时间，其单位为秒。

\[ \begin{aligned} I = \frac{V_S}{R}(1 - e^{-t/(L/R)}),\ &\frac{t}{(L/R)} = -\ln \big( \frac{1 - V_S/R}{V_S} \big) \\ V_R = IR = V_S(1 - e^{-t/(L/R)}),\ &\frac{t}{(L/R)} = -\ln \big( \frac{V_R - V_S}{V_S} \big) \\ V_L = L \frac{dI}{dt} = V_S \cdot e^{-t/(L/R)},\ &\frac{t}{(L/R)} = -\ln \big( \frac{V_L}{V_S} \big) \end{aligned} \]

运用基尔霍夫电压定律，对于闭合回路当中的电压进行求和，就可以得到 RL 电路的充电响应表达式：

\[ V_S = IR + L \frac{dI}{dt} \implies \frac{dI}{dt} + \frac{R}{L} \times I = \frac{V}{L} \]

求解上述的非齐次微分方程，初始条件为开关闭合之前的电流 \(I(0) = 0\)，由此就可以求解得到电流 \(I\) 的表达式：

\[ I = \frac{V_S}{R}(1 - e^{-t/(L/R)}) \]

将上面的 \(I\) 代入欧姆定律和电感电压的表达式，分别就可以得到电阻电压 \(V_R\) 与电感电压 \(V_L\)：

\[ \begin{aligned} & V_R = I \cdot R = V_S(1 - e^{-t/(L/R)}) \\ & V_L = L \cdot \frac{dI}{dt} = V_S \cdot e^{-t/(L/R)} \end{aligned} \]

这里假设电阻值为零，在没有电阻的情况下闭合开关，根据欧姆定律电流将会持续增大，最终使得自感电压与电源电压相等。如果电路当中存在电阻，那么欧姆定律就会限制电流的大小，此时 电感 \(L\) 上产生的反向感应电压，必须等于电源电压与电阻电压之差；当电流接近欧姆定律所限制大小的时候，这个感应电压将会变得非常小；由于反向电压在理论上不可能完全消失，电流也不会完全达到欧姆定律所限制的大小。所以在实际情况下，该差值较短时间内就能够降低到可以被忽略的水平。

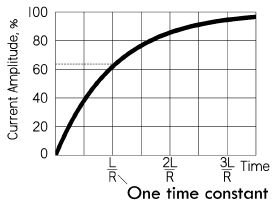
当电流达到最大值的 63.2% 时，所花费的时间就称为时间常数，其值 \(\tau\) 等于 \(\frac{L}{R}\)，单位为秒。每经过 1 个时间常数，电路都将会再传输 63.2% 的剩余电流，大约经过 5 个时间常数之后，就可以认为电流已经达到了最大值。

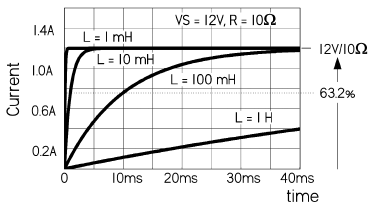
如果一个 RL 电路的电感为 10mH，串联电阻值为 10Ω，当该电路通电之后，电流达到最大值约需要经过 5 个时间常数，所以 \(t = 5 \tau = 5(L/R) = 5(10 \times 10^{-3}H) / 10Ω = 5.0 \times 10^{-3} 秒 = 50 毫秒\)。当电感系数增加到 1.0H 的时候，所需要的时间则会增加到 0.5 秒。由于电路里的电阻值不变，所以两种情况下电流的最大值都相同。但是增大电感系数之后，电流达到最大值所需要的时间将会变长。下图给出了电路在拥有相同电阻不同电感的情况下，电流的响应曲线：

LR 放电电路

断开开关之后，电感的磁场会随着电流的消失而消失，储存在磁场当中的能量将会被释放回电路。在开关断开的瞬间，由于感应电压与磁场的变化率呈正比，磁场骤降引发的感应电压通常比电源电压要大上许多倍，进而导致开关触点位置产生火花或者电弧。

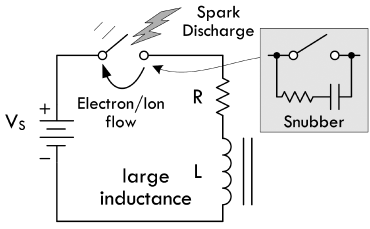
当电路里的电感系数以及电流很大的时候，就会在短时间之内释放较大的能量，导致开关触点烧蚀熔化。如果在开关触点两端串联上电容和电阻，就可以抑制火花或者电弧，这样用途的 RC 电路被称为缓冲电路。下图左侧的电路可以在不断开电路的情况下移除电源激励，此时电流将会遵循下图右侧的波形，以及接下来的方程进行衰减：

对于上述的 RL 放电电路，运用基尔霍夫定律，对闭合回路当中的电压进行求和，就可以得到如下的推导过程：

\[ V_S = IR + L \times \frac{dI}{dt} \implies \frac{dI}{dt} + \frac{R}{L} \times I = \frac{V}{L} \]

对于上述的非齐次微分方程进行求解，并且假设初始条件为开关闭合之前的电流 \(I(0)\)，就可以求解得到电流 \(I\)：

\[ I(0) = \frac{V_R}{R} \implies I = \frac{V_S}{R} \cdot e^{-t(L/R)} \]

同样将上面的电流 \(I\) 代入欧姆定律和电感电压表达式，就可以得到电阻电压 \(V_R\) 与电感电压 \(V_L\)：

\[ \begin{aligned} & V_R = I \cdot R = V_S \cdot e^{-t/(L/R)} \\ & V_L = L \cdot \frac{dI}{dt} = - V_S \cdot e^{-t/(L/R)} \end{aligned} \]

类似于之前介绍过的 RL 充电电路，RL 放电电路的电流响应也可以采用时间常数来进行表示。在 5 个时间常数以后，就可以认为电感放电结束。

本小节第 1 个电路里的开关断开，电流被切断，导致感性负载的磁场骤降，进而产生一个较大的同向感应电压。当该电压增大至一定程度时，开关触点之间的电压也将会变得很大，进而导致电火花的出现，此时的电流与电压响应曲线会比较复杂。而本小节第 2 个电路中的开关从位置 A 移动至位置 B，导致电源激励从电路当中断开，此时电流 \(I\) 与电阻电压 \(V_R\)、电感电压 \(V_L\) 表达式分别为：

\[ \begin{aligned} I = \frac{V_S}{R}e^{-t/(L/R)},\ &\frac{t}{(L/R)} = -\ln \big( \frac{I \times R}{V_S} \big) \\ V_R = IR = V_S \cdot e^{-t/(L/R)},\ &\frac{t}{(L/R)} = -\ln \big( \frac{V_R}{V_S} \big) \\ V_L = L \frac{dI}{dt} = - V_S \cdot e^{-t/(L/R)},\ &\frac{t}{(L/R)} = -\ln \big( \frac{V_L}{V_S} \big) \end{aligned} \]

该电路的电阻 \(R = 100Ω\) 电感 \(L = 20mH\)，而上面方程当中的 \(L/R = \tau\) 为时间常数，常数 e = 2.718。电流的单位为安培，电源电压 \(V_S\) 与电阻电压 \(V_R\) 以及电感电压 \(V_L\) 的单位都为伏特，电阻 \(R\) 的单位为欧姆，电感系数 \(L\) 的单位为亨利，而 \(t\) 表示接入电源之后的时间，单位为秒。

无论 RL 电路里的电感系数大小为多少，都会对输出信号造成影响。例如下图所示的 RL 电路当中，电感与电阻两端的输出信号，会随着电感系数的增大（放电时间延长），进而导致波形失真逐渐加剧：

接下来，把频率为 1.0kHz，周期为 \(T = \frac{1}{f} = \frac{1}{1000 Hz} = 1ms\)，电压为 0 ~ 5V 的方波电压源连接至电阻为 10Ω 的 RL 电路，然后增大电感系数，观察波形的变化过程：

1. 电感系数 \(L = 0.1mH\)，时间常数 \(\tau = \frac{0.0001H}{10Ω} = 0.01ms\)，此时 RL 电路的时间常数为周期的 1%，因而在方波由高到低和由低到高的变化过程当中，感应电压表现为窄尖峰波形。假设电感的充放电在 5 个时间常数（即 0.05ms）以后完成，即在半个周期（0.5ms）之内完成充放电，因而电阻电压的波形边缘会略带弧度：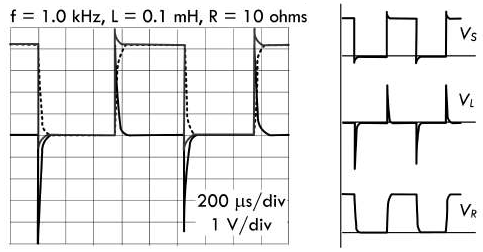

   

2. 电感系数 \(L = 1mH\)，时间常数 \(\tau = \frac{0.001H}{10Ω} = 0.1ms\)，此时 RL 电路的时间常数为周期的 10%，因而在电源电压的变化过程当中，感应电压呈指数规律进行升降的效果较为明显。其完全充放电所需的 5 个时间常数为 0.5ms，正好是周期的一半。所以在每半个周期里，电感都可以完全吸收、释放其磁场能量：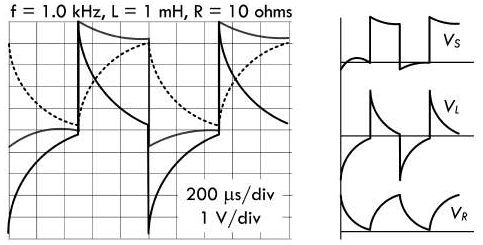

   

3. 电感系数 \(L = 10mH\)，时间常数 \(\tau = \frac{0.01H}{10Ω} = 1ms\)，此时 RL 电路的时间常数与方波周期相等，但由于需要 5 个时间常数（即 5ms）来完成充放电过程，所以感应电压近似为线性变化，其波形按照指数函数进行小幅度升降。在半个周期之内，电感的磁场并不能完全吸收、释放其磁场能量：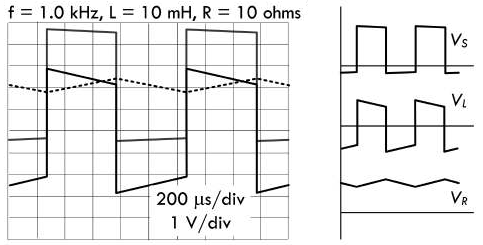

   

4. 电感系数 \(L = 1H\)，时间常数 \(\tau = \frac{1H}{10Ω} = 0.1s\)，此时 RL 电路的时间常数为周期的 100 倍，电感完全充放电所需的 5 个时间常数等于周期的 500 倍。换而言之，电感没有足够的时间来完成充放电。虽然波形仍然呈指数规律升降，但是实际只占据初始值的 \(\frac{1}{500}\)，其波形可以近似为一条直线：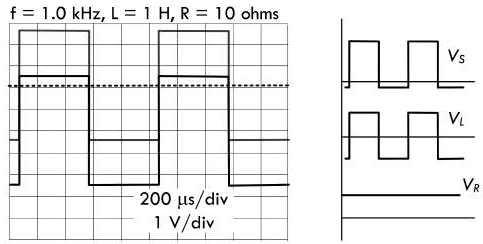

   

开关尖峰电压

携带有诸如继电器、螺线管、电动机等较大感性负载的电路当中，机械或者晶体管的开关操作经常会引发尖峰状的感应电压。即使电源电压较小的时候，所形成的尖峰电压也可以高达数百伏。尖峰电压会引发电弧，造成开关触点性能下降或者晶体管损坏。下图所示的电路，将一个可以让电流单向流动的二极管，并联至继电器的线圈两端，从而在需要断开电路时，为尖峰电压提供缓冲路径：

直导线电感

通电的直线导体（非线圈）周围都会存在磁场，因而也就存在着自感系数，一段非磁性材料制成的直导线电感值为：

\[ 电感 L = 0.00508 \times 导线长度 b \bigg[ \ln \bigg(\frac{2 \times 导线长度 b}{导线半径 a} \bigg) - 0.75 \bigg] \]

上面公式里的电感单位为毫亨 \(\mu H\)，导线半径 \(a\) 与导线长度 \(b\) 的单位为英尺（1 inch = 30.48 cm），而 \(\ln\) 为自然对数。

直导线的电感值较小，通常被称为寄生电感。低频时寄生电感的电抗为零，例如 10MHz 的时候，\(0.106 \mu H\) 电感的电抗仅为 6.6Ω；但是当频率上升至 300MHz 时，其电抗就会上升至不容忽视的 200Ω。因而在高频电路当中，应当尽可能的缩短元件的引脚端。由于导线总是与元件相互串联，一个元件的寄生电感可以通过在该元件上串联一枚数值相近的电感器来模拟。

注意：超高频率（30MHz ~ 300MHz）电路当中，由于集肤效应的存在，上面的公式会有一些微小的改变。当频率接近于无穷大时，上述公式中的常数 0.75 可以近似为 1。

互感现象

如果两个电感线圈沿着相同的轴线进行放置，那么流过线圈 1 的电流所形成的磁通将会通过线圈 2。当线圈 1 的磁场强度发生改变时，线圈 2 上将会产生感应电压。这个感应电压类似于自感电压，由于属于外部线圈 1 的作用结果，因而被称为互感电压，而这种现象就被称作互感。

上述两个线圈的关系称为感应耦合，它们靠得越近，互感就会越强。如果两个线圈间隔较远，或者并不处于相同的轴线上面，那么互感就会相对较弱，此时两个线圈称为松耦合。

互感系数的实际值与其最大值的比值，称为耦合系数，通常采用分数来进行表示。如果将一个空芯线圈缠绕在另一个空芯线圈的上面，那么两个线圈的耦合系数将会达到 0.6 ~ 0.7。如果将它们分开进行放置，那么耦合系数就会相对较小。当线圈绕制在闭合磁芯上面的时候，其耦合系数甚至可以达到 100%。

注意：互感原理主要应用于变压器当中，而在设计电路的时候，互感现象会产生一些不良后果。例如元件位置靠得太近的时候，或者感性负载、大电流交流电缆造成外部磁场波动的时候，电路当中就会出现错误的互感电压信号干扰。

电感的串联

当两个或者两个以上的电感器串联时（电感之间需要保持一定距离，避免相互之间的磁场干扰）：

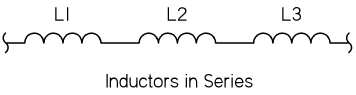
总电感量 \(L_{total}\) 等于每一个串联电感器上面的电感量之和：

\[ L_{total} = L_1 + L_2 + L_3 + ... + L_n \]

上述串联电感的计算公式，也可应用基尔霍夫电压定律推导得出，将电感 \(L_1\) 的电压记为 \(L_1 \frac{dI}{dt}\)，电感 \(L_2\) 的电压记为 \(L_2 \frac{dI}{dt}\)，电感 \(L_3\) 的电压记为 \(L_3 \frac{dI}{dt}\)，那么下面公式当中的 \((L_1 + L_2 + L_3)\) 部分就是串联等效电感：

\[ V = L_1 \frac{dI}{dt} + L_2 \frac{dI}{dt} + L_3 \frac{dI}{dt} = (L_1 + L_2 + L_3) \frac{dI}{dt} \]

电感的并联

当两个或者两个以上的电感器进行并联时（电感之间同样保持一定距离，避免相互之间的磁场干扰）：

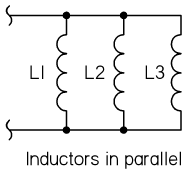
总电感量 \(L_{total}\) 的倒数就等于每一个并联电感器上面电感量的倒数之和：

\[ \frac{1}{L_{total}} = \frac{1}{L_1} + \frac{1}{L_2} + \frac{1}{L_3} + ... + \frac{1}{L_n} \]

如果当前只存在两个电感器进行并联，那么上述的计算公式就可以简化为如下形式：

\[ L_{total} = \frac{L_1 \times L_2}{L_1 + L_2} \]

该并联电感的计算公式，可以采用基尔霍夫电流定律推导获得。由于并联电流 \(I = I_1 + I_2 + I_3\)，并且电感 \(L_1\)、\(L_2\)、\(L_3\) 之间的端电压相等，各个并联电感器上的电流可以分别表示为 \(I_1 = \frac{1}{L_1} \int Vdt\)、\(I_2 = \frac{1}{L_2} \int Vdt\)、\(I_3 = \frac{1}{L_3} \int Vdt\)，那么电流 \(I\) 就可以表示为如下形式，其中的 \((\frac{1}{L_1} + \frac{1}{L_2} + \frac{1}{L_3})\) 部分就是并联等效电感：

\[ I = I_1 + I_2 + I_3 = \frac{1}{L_1} \int Vdt + \frac{1}{L_2} \int Vdt + \frac{1}{L_3} \int Vdt = \bigg( \frac{1}{L_1} + \frac{1}{L_2} + \frac{1}{L_3} \bigg) \int Vdt \]

▶【例题】下图所示电路的等效总电感值为 70mH，求解电感 \(L_2\) 的值 ？

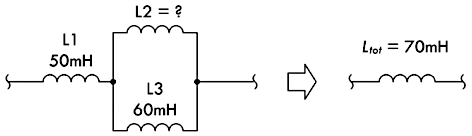
◉【解】根据上面电路图里的参数与题设条件，经过如下的一系列推导步骤，就可以计算出 \(L_2\) 的电感值等于 30mH：

\[ L_{total} = L_1 + \frac{L_2 \times L_3}{L_2 + L_3} \implies 70mH = 50mH + \frac{60mH \times L_2}{60mH + L_2} \implies L_2 = 30mH \]

电感与交流信号

当在理想电感器两端接入交流电压的时候，经过电感器的电流会滞后于电压，这与交流信号下电容器的特性正好相反。下图为理想电感电路当中的交流信号的电流、电压、功率曲线：

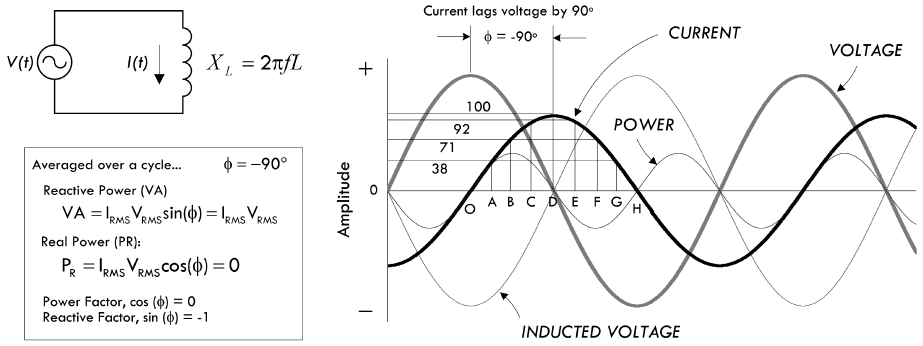
造成滞后的根本原因在于电感器产生了反向电压，由于反向电压的大小与电流的变化率呈正比：

1. 在 0 ~ A 时间段，电源电压为正向最大值，反向电压（感应电压）也为最大值，此时经过的电流最小，但是电流的变化率达到了 38% 的最大值；
2. 在 A ~ B 时间段，电流变化了 33%，感应电压与电源电压同步减小。该过程会在 B ~ C 与 C ~ D 时间段持续进行，随着电源电压以及感应电压趋于零，电流仅仅只增加了 8%；
3. 在 D ~ E 时间段，电源电压改变了方向，感应电压也会相应的改变方向。伴随着磁场的减小，电流开始返回电路，此时电流的方向与电源电压方向相反，但是仍然处于正向。随着电源电压在反方向继续增大，正向的电流值开始减小，当电源电压为反相最大值时电流为零；
4. 接下来，负半周的变化过程与正半周的情况相同，因而可以认为纯电感电路当中的交流信号，其电流总是滞后于电压 90°；

感抗

类似于容抗，感抗是电感与交流信号频率的综合效应，其单位也采用欧姆 Ω，具体的计算公式如下面所示：

\[ 感抗 X_L = 2 \pi \times 频率 f \times 电感 L \]

上述公式当中的 \(\pi = 3.1416\)，频率 \(f\) 的单位为赫兹 Hz，电感 \(L\) 的单位为亨利 H。除此之外，感抗还可以采用角频率来进行描述：

\[ 感抗 X_L = 角频率 \omega \times 电感 L \]

为了使得计算更加简便，可以采用余弦函数代替正弦函数，例如电源电压的表达式为 \(V_0 \cos (\omega t)\)，则电感元件上面经过的电流 \(I\) 等于：

\[ I = \frac{1}{L} \int Vdt = \frac{1}{L} \int V_0 \cos(\omega t) dt = \frac{V_0}{\omega L} \sin(\omega t) \]

当上面等式当中的 \(\sin(\omega t) = 1\) 的时候，电感上经过的电流将会达到最大值 \(I_0 = \frac{V_0}{\omega L}\)。峰值电压与峰值电流的比值具有欧姆 Ω 的量纲，其体现了反向感应电压抵抗正向电压的效应，这种效应就称之为感抗：

\[ X_L = \frac{V_0}{I_0} = \frac{V_0}{\frac{V_0}{\omega L}} = \omega L \]

当角频率 \(\omega\) 趋向于无穷大时，感抗 \(X_L\) 也将会趋于无穷大，此时电感相当于开路，说明电感会阻碍高频信号的通过。但当 角频率 \(\omega\) 趋于零的时候，感抗 \(X_L\) 也将会趋于零，说明低频信号可以轻松的通过。

注意：在理想电感通过直流信号的情况下，就不需要考虑到阻抗的概念。

下图分别为 \(1\mu H\)、\(10\mu H\)、\(100\mu H\) 电感器的感抗，伴随着频率进行变化的对数坐标图。可以看到其响应曲线呈线性。当频率增大的时候，对应的感抗也会随之呈正比增大：

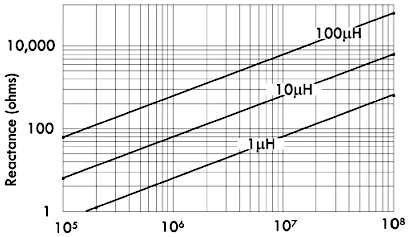
由于实际电感器的内部存在着寄生电阻与寄生电容，因而真实的感抗响应曲线将会比较复杂，下图为实际电感器的阻抗伴随着频率进行变化的曲线：

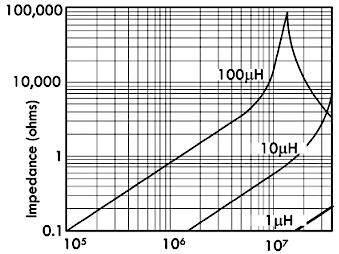
注意：当频率接近电路的振荡频率时，阻抗曲线就不会再呈现为线性，而是达到峰值之后就开始下降，后续振荡电路部分的内容将会对其进行更为详细的介绍。

实际电感模型

实际电感模型可以通过串联电感 \(L\)、串联电阻 \(R_{DC}\)、并联电容 \(C_P\)、并联电阻 \(R_P\) 四个无源理想元件来进行模拟：

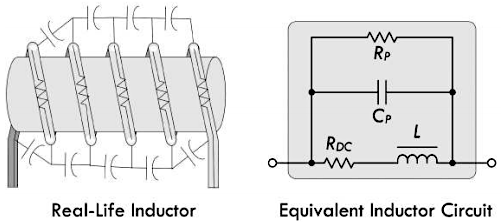
• 直流电阻 \(R_{DC}\) 表示的是电感通过直流信号时候的阻值，该参数通常由生产厂商的数据手册提供；
• 并联电阻 \(R_P\) 表示的是磁芯损耗，可以根据自谐振频率为 \(f_0\) 的时刻，电感的感抗为 0（即阻抗表现为纯电阻）求解得到，或者也可以通过品质因数 Q 进行求解；
• 并联电容 \(C_P\) 表示电感的线圈与引脚之间的分布电容；

当电感通过交流信号的时候，电感两端的电压将会发生变化，其作用等效于多个电容与电感线圈的并联。下图展示了分布电容与电感发生谐振时的曲线，低于谐振频率时阻抗呈感性，其值随着频率的增大而减小；而高于谐振频率时阻抗呈容性，其值会随着频率的增大而增大：

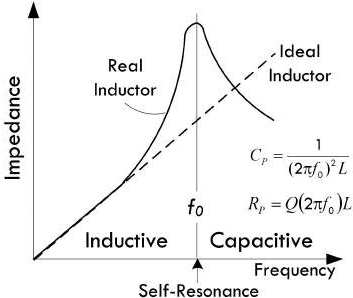
注意：实际电感器往往存在着多种形式的损耗，例如导线电阻损耗、磁芯损耗、集肤效应损耗。除此之外，当交流信号的频率增大时，电流将会集中到导体的表面，这种特性称为集肤效应，因而电感线圈还存在着集肤效应引发的损耗。

品质因数 Q

电容与电感这类储能元件的性质，都可以采用品质因数 Q 来进行描述，其值等于储能元件存储的能量（感抗）与消耗能量（电阻）的比值：

\[ 品质因数 Q = \frac{电抗 X}{电阻 R} \]

注意：上述方程当中的品质因数 Q 没有量纲，而 \(X\) 为电抗（感抗或者容抗），电阻 \(R\) 表征电感元件实际损耗的全部能量。

电容器通常具备较高的 Q 值，例如陶瓷电容器的 Q 值可以达到 1200 以上。而电感的品质因数为 \(Q = \frac{2 \pi f L}{R_{DC}}\)，当电路当中同时包含有电感和电容时，电感的 Q 值并不会等于电容的 Q 值。

注意：多数情况下，电路都会要求使用更高品质因数的电感，然而有些电路则会要求使用比较特殊的 Q 值参数。

感性分压器经常被应用在输入交流信号的电路当中，根据电阻分压的原理，交流输入电压将会按照两个电感的电阻关系进行分配，具体请参考下面的电路图与公式：

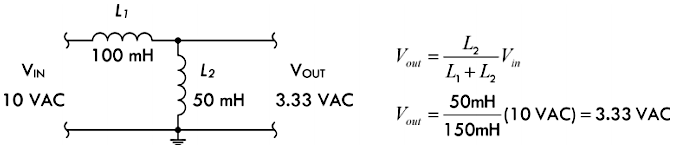
注意：上述电路的输出电压与输入频率无关，但是如果电感器的感抗在指定工作频率上不够高（即电感值不够大），那么并联元件 \(L_2\) 将会如同短路，从而产生非常大的电流。

电子学当中，电感器的基本功能是以磁场的形式存储电量，电感器与电容器等其它元件组合起来，就可以形成用于滤除特殊频率信号的滤波器。除此之外，两个或者两个以上的耦合线圈，还可以构成用于对交流电压进行升压与降压的变压器。而在开关电源当中，电感器可以控制稳压器在开关频率的特定部分进行充电，而在剩余的周期内进行放电，充放电比例决定了输出与输入电压的比值。

正弦电路分析

下图所示的电路当中包含有电阻、电容、电感，以及正弦电压源：

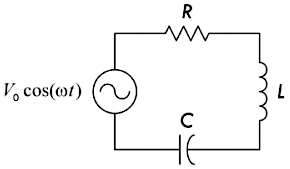
应用基尔霍夫电压定律就可以得到下面的推导过程：

\[ V_0 \cos (\omega t) = IR + L \frac{dI}{dt} + \frac{1}{C} \int I dt \implies L\frac{d^2 I}{dt^2} + R \frac{dI}{dt} + \frac{1}{C} I = - \omega V_0 \sin(\omega t) \]

上述等式是一个二阶线性非齐次常微分方程，通过参数变换或者待定系数法求解方程，并将求解得到的电流代入电阻、电容、电感的电压与电流关系方程，通过繁杂的数学运算就可以求解得到各个元件上的电压。上面这个电路相对较为简单，而对于下图这种较为复杂的电路，如果继续运用基尔霍夫定律对回路与节点列写微分方程，那么涉及的运算将会变得极为复杂：

注意：通过复阻抗的概念以及相应的复数运算，就可以完全规避复杂的微分方程求解过程。

复阻抗分析正弦电路

一个采用正弦电源作为激励的电路，所有的电压与电流都是正弦量，它们会与正弦电压源的输出同频率变化。如果电路当中存在电容器和电感器，那么电压与电流的幅值与电压源的幅值成正比，而电压与电流的波形相对于电压源的波形存在着相位差。利用正弦电路的电压与电流都属于同频率正弦量的特点，就可以避免以求解微分方程的方式来分析动态电路。

叠加原理指出在具有多个正弦电源的线性电路当中，任意一个支路上的电流等于各个电源单独作用时产生的电流之和。利用基尔霍夫定律可以证明这个结论，将基尔霍夫定律应用于线性电路，从而得到一组线性方程，将它们简化为只包含有 1 个未知数的单一方程，如果未知量是支路电流，那么可以将其表达为具有适当系数的各个电源的叠加。换而言之，就是无需再计算时间相关的未知量，由于这些未知量的形式总是 \(\cos(\omega t + \varPhi)\)，因而只需要计算其峰值（或者 RMS 均方根值）以及相位角，再运用叠加原理进行求解即可。

具有相同频率、不同相位的两个正弦波叠加，得到的将会是一个具有相同频率的新正弦波：

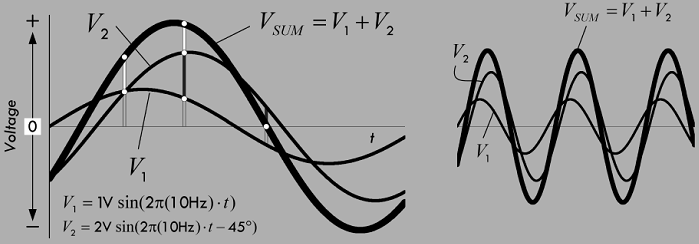
而对于频率不同的正弦波，叠加之后得到的将不再是一个正弦波：

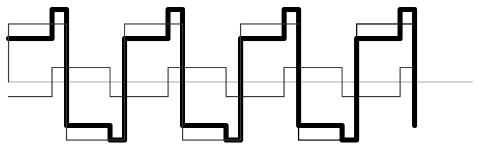
频率相同、相位不同的两个方波，叠加之后所获得的并不一定就是一个方波：

本文在《数学预备知识》章节，介绍过采用复数表示正弦量的相关概念。例如，当 \(\theta\) 在 \(0° \sim 360°\) 范围变化时，复数的三角形式 \(z = r \cdot \cos \theta + j \times r \cdot \sin \theta\) 在复平面上的轨迹是一个圆周。如果取 \(z\) 相对于 \(\theta\) 的实部来绘制曲线，就可以得到一个正弦波；而通过改变 \(r\) 的值，就可以改变正弦波的幅值；让 \(\theta\) 乘以一个系数，就可以改变正弦波的频率；让 \(\theta\) 加上一个数值（度或者弧度)，就能够与同频率的正弦波产生相位差。

注意：如果将 \(\theta\) 替换为 \(\omega t\)（其中 \(\omega = 2 \pi f\)），把 \(r\) 替换为 \(V_0\)，同时为 \(\omega t\) 添加相位差，就可以得到以复数形式表示的电压源，采用类似的办法也可以表示电流源。

相比于正弦函数，复数的优势在于可以采用多种形式（直角坐标系、三角、指数、极坐标）进行表示，从而简化叠加过程当中的数学运算。例如，将复数转化成直角坐标形式之后，就可以容易的进行加减运算，而转化为指数形式与极坐标形式，则可以很容易的进行乘除运算。

电流与电压的值事实上都属于实数，并不存在虚数的电压与电流。之所以存在虚部是因为需要引入相位的概念，所以采用复数形式进行叠加之后，所得到的最终结果必须转换为实数，即必须将复数结果转换为三角形式、指数形式、极坐标形式，并且移除虚部。例如下面等式当中的电压采用 RMS 均方根值，将等式左侧的复数，转换为右侧的指数和极坐标形式：

\[ V(t) = 5V + j10V \implies \sqrt{(5.0V)^2 + (10.0V)^2} e^{j 63.4°} \approx (11.2V) e^{j 63.5°} = 11.2V \angle 63.5° \]

经过上述推导过程，就可以得到电压 \(V(t)\) 的 RMS 值为 11.2V，由于相位 \(\angle 63.5°\) 往往无关紧要，所以这里直接将其忽略。

复数表示正弦电压源

假设正弦电压为 \(V_0 \cos (\omega t)\)，其中 \(\omega = 2 \pi f\)，将其转换为 \(V_0 \cos (\omega t) + j V_0 \sin(\omega t)\)，这个等式当中的 \(j V_0 \sin(\omega t)\) 是没有任何物理意义的虚数，虽然不会影响到实际的电压表达式，但是在叠加计算过程当中会使用到它。接下来为了便于计算，需要使用欧拉公式 \(e^{j \theta} = r \cos(\theta) + jr \sin(\theta)\) 将三角形式转换为指数形式 \(V_0 \cdot e^{j(\omega t)}\)，或者极坐标形式 \(V_0 \angle (\omega t)\)。

上述的电压可以在复平面当中，采用一个角频率为 \(\omega\)，并且沿着逆时针方向旋转的矢量来进行表示。其中，矢量长度表示电压 \(V_0\) 的最大值，而该矢量在实轴的投影表示 \(V\) 的实部或者瞬时值，在虚轴上的投影表示的则是 \(V\) 的虚部:

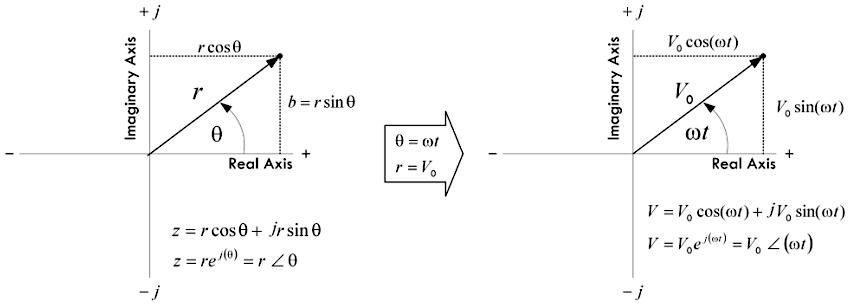
得到电压的复数表达式之后，分别将其代入电阻（\(I = \frac{V}{R}\)）、电容（\(I = C \frac{dV}{dt}\)）、电感（\(I = \frac{1}{L} \int Vdt\)）的表达式，进而分别得到电流的复数表达式，比较每种元件的电流以及电压的相位差，就能够得到下面的示意图：

• 电阻：电压与电流同相，相位差 \(\varPhi = 0°\)，该特性也可以在复平面上表示，其中电压与电流的矢量都具有相同的辐角，两者都以角频率 \(\omega = 2 \pi f\) 沿逆时针方向进行旋转；
• 电容：电流的相位大于电压有 +90°，即电流超前于电压有 90°，通常规定相位差 \(\varPhi\) 为从电流矢量指向电压矢量的角度，当 \(\varPhi\) 为正时电流超前，当 \(\varPhi\) 为负时电流滞后；
• 电感：电流的相位大于电压有 -90°，即电流滞后于电压有 90°；

这种在复平面上采用电压与电流的幅值与相位角表示的图形称为相量图，相量与依赖于时间的数学函数不同，它只是提供了某一个瞬间或时刻的相位与幅值。接下来，再介绍一种重要的交流电路分析方法，如果分别将电阻、容抗、感抗元件上的电压除以电流，就可以得到下图所示的结果：

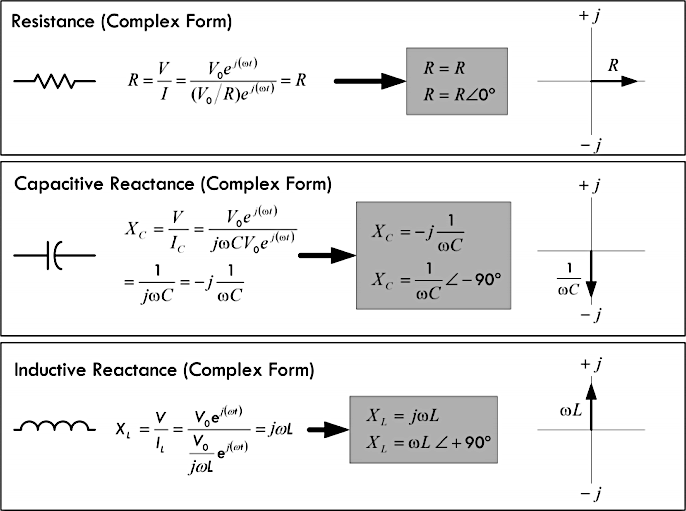
注意：上图当中的 \(V_0 \cdot e^{j(\omega t)}\) 项被消去，得到电阻、容抗、感抗的复数形式。这些表达式只是频率的函数，而与时间无关，从而避免求解微分方程。

正弦激励电路当中，把容抗与感抗表示为复数，就可以将电容和电感视为频率敏感的电阻，采用这些电阻替代直流电路当中的电阻，再将直流电源切换为正弦电源，并将所有的电压、电流、电阻、阻抗转换为复数形式，分别代入欧姆定律、基尔霍夫定律、戴维南定理等电路定理建立方程，通过简单的复数运算就能够进行求解。例如交流欧姆定律可以表示为 \(V(\omega) = I(\omega) \times Z(\omega)\)，其中的 \(Z\) 就是复阻抗，一种以复数形式描述元件对于电流阻碍作用的方法。复阻抗可以只是电阻、容抗、感抗，也可以是电阻与电抗元件的组合：

\[ \begin{cases} 电阻 &V_R = I_R \times R \\ 电容 &V_C = I_C \times X_C = I_C \big( - j \frac{1}{\omega C} \big) = - j \frac{I_C}{\omega C} = \frac{I_C}{\omega C} \angle -90° \\ 电感 &V_L = I_L \times X_L = I_L (j \omega L) = j I_L \omega L = I_L \omega L \angle + 90° \\ 复阻抗 &V_Z = I_Z \times Z \end{cases} \]

下图展示了之前讨论过的正弦电压源的相量表示，以及电阻、电容、电感的复阻抗：

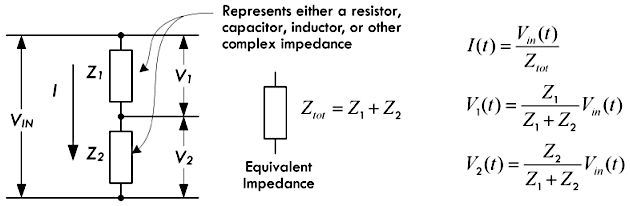
将复阻抗视为频率敏感的电阻，通过串联电阻的等效公式，就可以求解得到复阻抗串联之后的等效复阻抗 \(Z_{total}\)：

\[ Z_{total} = Z_1 + Z_2 + Z_3 + ... + Z_N \]

换而言之，之前的直流分压电路，可以转变成一个交流分压电路：

相应的，将 \(N\) 个复阻抗进行并联，其等效阻抗 \(Z_{total}\) 的表达式如下所示：

\[ Z_{total} = \frac{1}{\frac{1}{Z_1} + \frac{1}{Z_2} + \frac{1}{Z_3} + ... + \frac{1}{Z_N}} \]

特别的，如果当前只有两个复阻抗进行并联，那么上述公式可以简化为下面的形式：

\[ Z_{total} = \frac{Z_1 Z_2}{Z_1 + Z_2} \]

同样的，之前的直流分流电路，也可以转变为一个交流分流电路：

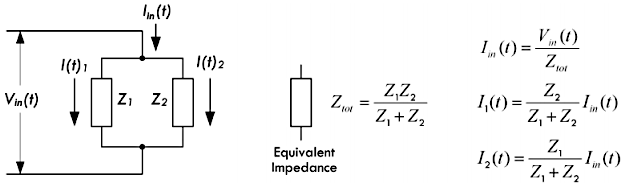
更为重要的是，可以将复阻抗代入基尔霍夫电压定律，通过建立回路方程来求解拥有多个节点的复杂电路：

▶【例题】下图的 RL 串联电路由一个输出电压为 12VAC（RMS 均方根值），频率为 60Hz 的电源激励，已知电路当中的电感 \(L = 265mH\)，电阻 \(R = 50Ω\)，求解 \(I_S\)、\(I_R\)、\(I_L\)、\(V_R\)、\(V_L\)，以及视在功率、有功功率、无功功率、功率因数？

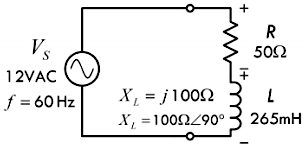
◉【解】首先，计算出感抗 \(X_L\)：

\[ X_L = j \omega L = j(2 \pi \times 60Hz \times 265 \times 10^{-3} H) = j 100Ω \]

◉【解】因为该电路当中的电阻与电感串联，所以采用直角坐标形式的复数相加，进而得到等效阻抗 \(Z\)：

\[ Z = R + X_L = 50 Ω + j100 Ω \]

◉【解】接下来，再将上面求解得到的等效阻抗 \(Z\) 转换为极坐标形式：

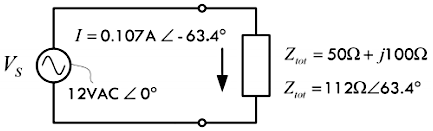
\[ Z = \sqrt{50^2 + 100^2} \angle \arctan \big( \frac{100}{50} \big) = 112Ω \angle 63.4° \]

◉【解】利用交流欧姆定律，就可以求解得到电流 \(I_S\)：

\[ I_S = \frac{V_S}{Z_{total}} = \frac{12 VAC \angle 0°}{112Ω \angle 63.4°} = 0.107A \angle -63.4° \]

◉【解】上面等式当中的 -63.4° 表示电流滞后于电源电压，由于串联电路当中 \(I = I_R = I_L\)，利用交流欧姆定律和分压公式就可以求解出电阻 \(R\) 与电感 \(L\) 两端的电压：

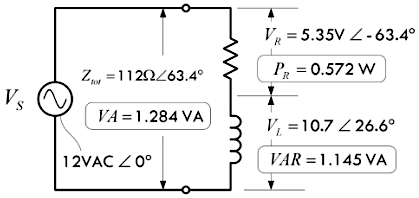
\[ \begin{cases} V_R = I \times R = (0.107A \angle -63.4°)(50Ω \angle 0°) = 5.35 VAC \angle -63.4° \\ V_L = I \times X_L = (0.107A \angle -63.4°)(100Ω \angle 90°) = 10.7 VAC \angle 26.6° \end{cases} \]

◉【解】以上步骤计算的是当 \(t = 0\) 时刻，电源电压 \(V_S = 12 VAC \angle 0°\) 情况下的值。如果需要绘制精确的波形，那么就需要将 \(\omega t\) 代入电源电压的表达式，并且将有效值乘以 1.414 得到 \(V_S = 17.0V \angle(\omega t)\)，该结果描述了电压随着时间的连续变化过程。接着再将这个结果转换为三角形式，去掉虚部就可以得到 \(V_S = 17.0 V \cos (\omega t)\)。参照电源电压 \(V_S\) 的推导过程，将其它电压与电流的波形全部列写为三角形式，再代入相应的峰值与相位角，就可以获得如下的波形与计算结果：

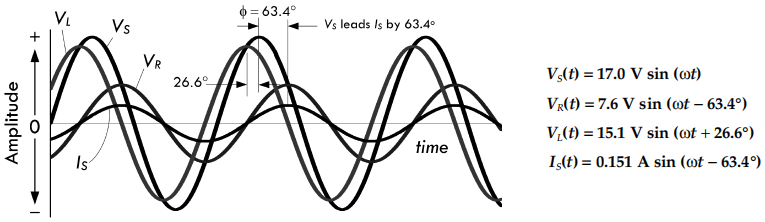
注意：峰值电压与电流等于其有效值乘以 1.414，例如 \(V_P = 1.414 \times V_{RMS}\)。

◉【解】根据上述推导结果，还可以获得该电路上面总阻抗的视在功率 \(VA\)、电阻消耗的有功功率 \(P_R\)、电感上的无功功率 \(VAR\)、功率因数 \(PF\)，接下来的章节将会逐一介绍这些内容：

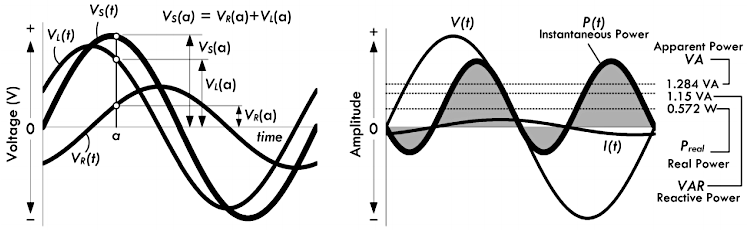
\[ \begin{cases} 总阻抗的视在功率 VA &= I_{RMS} \times V_{RMS} = (0.107A) \times (12 VAC) = 1.284 VA \\ 电阻消耗的有功功率 P_R &= I_{RMS}^2 R = (0.107A)^2 \times (50Ω) = 0.572 W \\ 电感上的无功功率 VAR &= I_{RMS}^2 X_L = (0.107A)^2 \times (100Ω) = 1.145 VAR \\ 功率因数 PF &= \frac{P_R}{VA} = \cos(\phi) = \cos(-63.4°) = 0.45 \end{cases} \]

注意：上述方程当中的 \(\phi\) 表示的是 \(V_S\) 与 \(I_S\) 之间的相位差。

上述示例当中，电阻电压 \(V_R\) 与电感电压 \(V_L\) 的代数和等于 \(5.35VAC + 10.70VAC = 16.05 VAC\)，该结果要大于电源电压 \(V_S = 12VAC\)，似乎并不满足基尔霍夫电压定律。这是由于没有考虑到相位角的因素造成的，纳入相位角之后的正确计算结果如下所示：

\[ \begin{aligned} V_{total} &= V_R + V_L = (5.35 VAC \angle - 63.4°) + (10.70 VAC \angle 26.6°) \\ &= 2.4 VAC - j 4.8 VAC + 9.6 VAC + j 4.8 VAC \\ &= 12 VAC \end{aligned} \]

下图当中的电压信号波形，非常直观的展示了波形的幅度与相位之间的对应关系：

视在功率

对于含有电阻、电感、电容元件的复杂电路，将之前介绍过的功率定理 \(P = I_{RMS} \times V_{RMS}\) 当中的 \(P\) 更换为 \(VA\)，就可以得到视在功率的计算公式：

\[ 视在功率 VA = I_{RMS} \times V_{RMS} \]

可以看到视在功率 VA 的计算公式与普通交流功率的计算公式相同，之所以使用 VA 而不使用 P，是由于计算出的功率值并不只是消耗了有功功率，因而不能使用以瓦特作为单位的有功功率来进行表示，而应当使用伏安 VA 作为其单位。

视在功率同时包含了电阻消耗的有功功率和无功功率。其中，有功功率是电流经过电阻时所产生的热损耗，其单位为瓦特 W，可以由交流欧姆定律代入功率定理之后得到的方程进行定义：

\[ 有功功率 P_R = I^2_{RMS} R \]

而无功功率不表示功率的消耗，其与电感器当中储存的磁场能量，以及电容器当中储存的电场能量存在着联系。当电感器的磁场减弱或者电容器进行放电时，它们当中储存的能量又会释放回电路当中。无功功率采用乏 VAR 来作为其单位，把上述欧姆功率定理当中的电阻或阻抗部分更换为电抗 \(X\)，就可以得到无功功率的定义：

\[ 无功功率 VAR = I^2_{RMS} X \]

为了简化计算过程，下面直接给出无功功率、有功功率、视在功率之间相互进行转换的关系式：

\[ 视在功率 VA = \sqrt{有功功率 P_R^2 + 无功功率 VAR^2} \]

功率因数

功率因数也是一种用于描述视在功率和无功功率的术语，电路的功率因数 \(PF\) 等于电路消耗的功率与视在功率的比值，通常以百分数 \(\%\) 格式来进行表示：

\[ 功率因数 PF = \frac{电路消耗功率 P_{consumed}}{视在功率 P_{apparent}} = \frac{P_R}{VA} \]

纯电阻电路的功率因数等于 \(100\% = 1\)，而纯电抗电路的功率因数则等于 \(0\)。由于功率因数总是为正数，所以必须明确的标识当前电压与电流之间的相位关系是超前还是滞后。除此之外，功率因数还可以表示为电压与电流之间相位差 \(\phi\) 的形式：

\[ 功率因数 PF = \cos \phi \]

除了功率因数之外，还有另外一个用于描述电抗当中无功功率所占百分比的术语，称为无功因数：

\[ RF = \frac{P_{reactive}}{P_{apparent}} = \frac{无功功率 VAR}{视在功率 VA} = \sin(\phi) \]

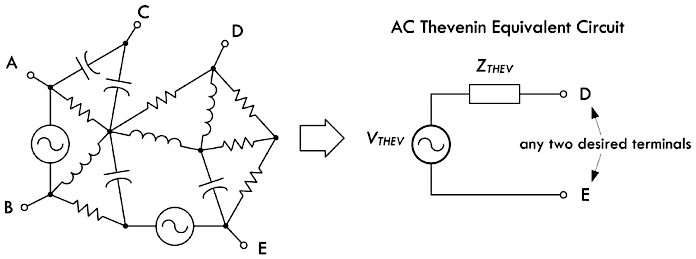
交流电路戴维南定理

戴维南定理同样可以应用于交流线性电路的分析，对于任意包含有电阻、电容、电感元件的复杂网络，都可以等效为一个正弦电压源与复阻抗的串联。例如求解复杂正弦电路当中两点之间的电压，或者某个元件上的电流与电压，只需要移除该元件，并求解出戴维南等效电压 \(V_{THEV}(t)\)，再将原来的正弦电源直接采用导线进行短路，进而求解出戴维南等效复阻抗 \(Z_{THEV}(t)\) 及其对应的戴维南等效电路。下图左侧是一个包含有电阻、电容、电感元件的复杂电路，而右侧是该电路所对应的戴维南等效电路：

▶【例题】求解下图所示电路当中流过电阻的电流 \(I_R\) ？

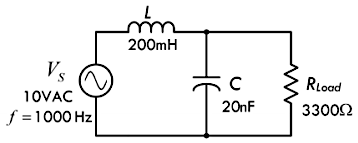
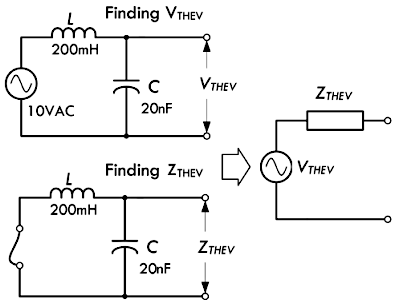
◉【解】首先，移除电阻，使得电路成为拥有两个外接端子的黑盒子：

◉【解】然后，再分别计算其容抗 \(X_C\) 与感抗 \(X_L\) ：

\[ \begin{aligned} &X_L = j \omega L = j(2\pi \times 1000Hz \times 200 \times 10^{-3}) = j 1257Ω \\ &X_C = - j \frac{1}{\omega C} = -j \frac{1}{2\pi \times 1000Hz \times 20 \times 10^{-9}F} = -j 7958Ω \end{aligned} \]

◉【解】接下来，运用交流分压公式计算出开路电压，也就是戴维南等效电压 \(V_{THEV}\)：

\[ \begin{aligned} V_{THEV} = V_C &= \bigg( \frac{X_C}{X_C + X_L} \bigg) \times V_S = \bigg( \frac{-j 7958 Ω}{-j 7958 Ω + j 1257 Ω} \bigg) \times 10 VAC \\ &= \bigg( \frac{7958 \angle -90°}{6701 \angle -90°} \bigg) \times 10 VAC = 11.88 VAC \angle 0° \end{aligned} \]

◉【解】再将正弦电源短路，得到其等效阻抗 \(Z_{THEV}\) 为电容与电感的并联：

\[ \begin{aligned} Z_{THEV} &= \frac{X_C \times X_L}{X_C + X_L} = \frac{-j7958Ω \times j1257Ω}{-j7958Ω + j1257Ω} \\ &= \frac{(7958Ω \angle -90°) \times (1257Ω \angle -90°)}{(6701Ω \angle -90°)} = \frac{10003206Ω^2 \angle 0°}{6702Ω \angle -90°} \\ & = 1493 Ω \angle 90° = j(1493)Ω \end{aligned} \]

◉【解】最后，把负载电阻与戴维南等效电路进行连接，得到如下的等效电路：

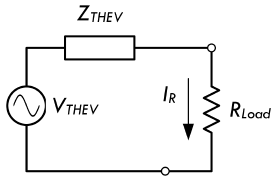
◉【解】根据戴维南等效电压 \(V_{THEV}\) 与电阻 \(R\) 的串联关系，就可以求解出总阻抗 \(Z_{total}\)：

\[ Z_{total} = R + Z_{THEV} = 3300Ω + j 1493 Ω = 3622 Ω \angle 24.3° \]

◉【解】基于交流欧姆定律，就可以求解得到经过电阻的电流 \(I_R\) 等于：

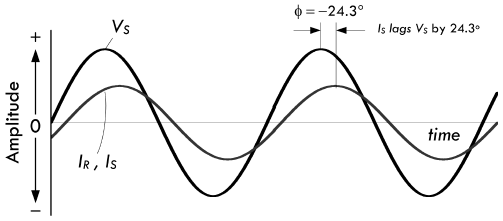
\[ I_R = \frac{V_{THEV}}{Z_{total}} = \frac{11.88 VAC \angle 0°}{3622Ω \angle 24.3°} = 3.28mA \angle -24.3° \]

◉【解】上述的计算结果表明，电阻上的电流 \(I_R\) 等于 3.28mA，并且滞后于电源电压 24.3°。如果需要将瞬时值转换为时间相关的实数函数，那么就要把 \(\omega t\) 添加到每一个相位角表达式，并且将 RMS 值转换为真实值：

◉【解】根据上述的计算结果，还可以求解得到该电路对应的视在功率、有功功率、无功功率、功率因数：

\[ \begin{cases} 视在功率 VA &= I_S^2 \times Z_{total} = (0.00328 A)^2 \times 3622 Ω = 0.039 VA \\ 有功功率 P_R &= I_R^2 \times R = (0.00328 A)^2 \times 3300 Ω = 0.035 W \\ 无功功率 VAR &= I_R^2 × Z_{THEV} = (0.00328 A)^2 \times 1493 Ω = 0.016 VAR \\ 功率因数 PF &= \frac{P_R}{VA} = \cos(\phi) = \cos(-24.3)° = 0.91(滞后) \end{cases} \]

谐振电路

如果在 LC 电路的两端电路添加正弦电压源，那么当电源的频率等于谐振频率时，就会发生一些有趣的现象。

LC 串联谐振

下图所示的 LC 串联电路的谐振角频率 \(\omega_0 = 1 \sqrt{LC}\) 或者等效谐振频率 \(f_0 = \frac{1}{2\pi/LC}\) 的时候，该 LC 电路的等效阻抗将会趋于零，即相当于短路，此时流过电源的电流达到最大值。理想状况下，这个电流将会趋于无穷大，但是实际上电路内电阻会将其限制在一定的范围。

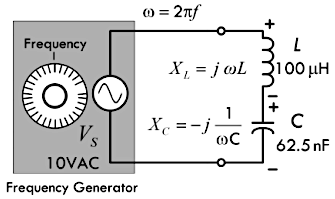
这里先求解出上述电路的等效阻抗，由于其频率未知，因而等效阻抗 \(Z_{total}\) 必须被视为一个变量：

\[ 等效阻抗 Z_{total} = 感抗 X_L + 容抗 X_C = j \omega L - j \frac{1}{\omega C} = j \bigg(\omega L - \frac{1}{\omega C} \bigg) \]

这个等效阻抗 \(Z_{total}\) 对应的极坐标形式如下面所示（任意数除以 0 的反正切为 90°，所以下面的阻抗相位角也等于 90°）：

\[ Z_{total} = \bigg( \omega L - \frac{1}{\omega C} \bigg) \angle 90° \]

此时，经过并联等效阻抗 \(Z_{total}\) 的电流 \(I\) 为：

\[ I = \frac{V_S}{Z_{total}} = \frac{10 VAC \angle 0°}{\omega L - \frac{1}{\omega C}} \angle -90° = \bigg[ \frac{10 VAC}{\omega L - \frac{1}{\omega C}} \bigg] \angle -90° \]

如果代入电感 \(L = 100 \mu H\)、电容 \(C = 62.5nF\)、角频率 \(\omega = 2 \pi f\)，并且不考虑相位角的因素，那么总阻抗 \(|Z_{total}|\) 与电流 \(|I|\) 分别等于：

\[ \begin{cases} |Z_{total}| = 6.28 \times 10^{-4} f - \frac{2546479}{f} Ω \\ |I| = 10 VAC \div \big[ 6.28 \times 10^{-4} f - \frac{2546479}{f} \big]Ω \end{cases} \]

可以看到，阻抗与电流都属于频率的函数，其波形如下图所示：

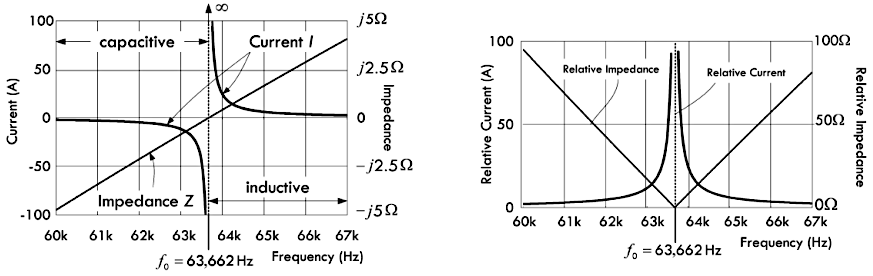
值得注意的是，当上述方程当中的频率等于谐振频率 \(f_0 = \frac{1}{2\pi \sqrt{LC}} = \frac{1}{2\pi \sqrt{(100 \times 10^{-6}H)(62.5 \times 10^{-9}F)}} = 63663 Hz\) 的时候，其阻抗等于零，同时电流趋于无穷大（实际情况下，电路内阻会限制电流大小）。电路发生谐振时，感抗与容抗的大小相等相位相反，具体请参见如下方程：

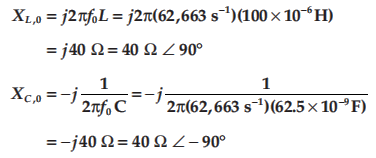
注意：LC 串联电路在发生谐振时，电容与电感两端的电压大小相等相位相反，意味着它们串联之后的有效电压降等于零，两端的阻抗也就一定等于零。

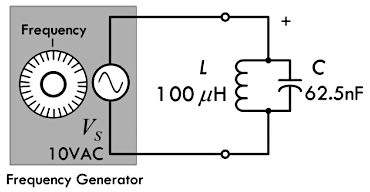
LC 并联谐振

下图所示并联 LC 电路的谐振角频率 \(\omega_0 = \frac{1}{\sqrt{LC}}\)，等效谐振频率 \(f_0 = \frac{1}{2\pi / \sqrt{LC}}\)，与 LC 串联电路谐振频率的表达式相同，但是作用的效果却完全相反，发生谐振时不再是阻抗趋于零，电流趋于无穷大。而是电阻趋于无穷大，电流趋于零，即相当于开路。实际情况下，由于电路当中内电阻、寄生电容、寄生电感的存在，这种开路现象并不会真实发生。

\[ 等效阻抗 Z_{total} = \frac{感抗 X_L \times 容抗 X_C}{感抗 X_L + 容抗 X_C} = \frac{(j \omega L)(-j \frac{1}{\omega C})}{j \omega L - j \frac{1}{\omega C}} = \frac{\frac{L}{C}}{j(\omega L - \frac{1}{\omega C})} = -j \frac{\frac{L}{C}}{(\omega L - \frac{1}{\omega C})} \]

将上述结果改写为极坐标形式（任意负数除以 0 的反正切为 -90°，所以下面的阻抗相位角也等于 -90°）：

\[ Z_{total} = \frac{\frac{L}{C}}{(\omega L - \frac{1}{\omega C})} \angle -90° \]

此时，流入并联阻抗的电流等于 \(I\)：

\[ I = \frac{V_S}{Z_{total}} = \frac{10 VAC \angle 0°}{\frac{L/C}{\omega L - 1 / \omega C}\angle - 90°} = \bigg[ \frac{10 VAC}{\frac{L/C}{(\omega L - 1 / \omega C)}} \bigg] \angle 90° \]

同样代入电感 \(L = 100 \mu H\)、电容 \(C = 62.5nF\)、角频率 \(\omega = 2 \pi f\)，如果不考虑相位角，那么总阻抗 \(|Z_{total}|\) 和电流 \(|I|\) 分别为：

\[ \begin{cases} Z_{total} = 1600 \div \big(6.28 \times 10^{-4} - \frac{1}{3.92 \times 10^{-7}} \big) Ω \\ I = 0.00625 \times \big(6.28 \times 10^{-4} - \frac{1}{3.92 \times 10^{-7}} \big) A \end{cases} \]

可以看到，阻抗与电流也同样是频率的函数，对应的波形如下图所示：

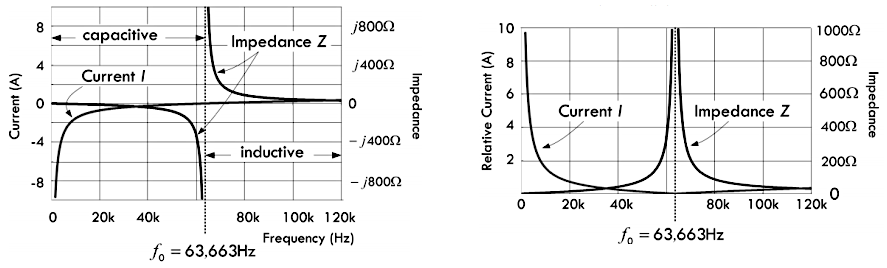
当上述方程当中的频率等于谐振频率 \(f_0 = \frac{1}{2\pi \sqrt{LC}} = \frac{1}{2\pi \sqrt{(100 \times 10^{-6}H)(62.5 \times 10^{-9}F)}} = 63663 Hz\) 的时候，其阻抗趋于无穷大，同时电流等于零。当频率趋近于零的时候，电感相当于短路，电流趋于无穷大；而当频率趋近于无穷大的时候，电容也相当于短路，同样会导致电流趋于无穷大（实际情况下，电路内阻、寄生电感、寄生电感会限制电流的大小）。

发生谐振时，由于电容 \(C\) 和电感 \(L\) 的阻抗 \(X_C = X_L\) 与电压 \(V_C = V_L\) 相等，但是相位相反。由此可知，流过电感 \(L\) 与电容 \(C\) 的电流同样大小相等方向相反。即流过电感的电流从电容上端流入，经过电容之后又从电感的下端流入，下一个时刻电流发生反相，能量沿着相反的方向释放。此时，电容与电感的作用类似于振荡器，来回传递相同的能量，该能量的大小取决于电感与电容的大小，这种在 LC 回路当中来回流动的电流被称为循环电流。此时由于电源两端的电位差较小，所以经过电源的电流也比较小。换而言之，如果希望 LC 电路提供一个外部电流，那么就意味着电感与电容元件必须存在电位差。但是发生谐振的时候，由于流过电感与电容的电流相等而方向相反，因而无法对外提供电流。

▶【例题】如果一个谐振电路的电感为 \(5.0 \mu H\) 而电容为 \(35pF\)，试求解电路的谐振频率 ？

◉【解】根据题设条件，该电路的谐振频率 \(f_0\) 等于：

\[ f_0 = \frac{1}{2 \pi \sqrt{LC}} = \frac{1}{2 \pi \sqrt{(5.0 \times 10^{-6}) \times (35 \times 10^{-12})} } = 12 \times 10^6 Hz = 12 MHz \]

▶【例题】如果一个谐振电路的电感为 \(2.0 \mu H\)，如果谐振频率为 \(21.1 MHz\)，试求解电路当中电容的值 ？

◉【解】根据题设条件，这个电路当中电容 \(C\) 的值等于：

\[ f_0 = \frac{1}{2 \pi \sqrt{LC}} \implies C = \frac{1}{L} \big( \frac{1}{2 \pi f_0} \big)^2 = \frac{1}{2.0 \times 10^{-6}H} \big[ \frac{1}{2 \pi (21.1 \times 10^6 Hz)} \big]^2 = 2.85 \times 10^{-11} F = 28.5F \]

注意：上述公式可以在元件允许的误差范围之内，计算出相应的频率与元件参数。除了谐振频率之外，谐振电路还具有阻抗、带宽、串联谐振电路当中元件之间的压降、并联谐振电路中的循环电流 等重要特性。

RLC 串联谐振

前面讨论的 LC 串联谐振电路、LC 并联谐振电路都属于理想电路，由于电路元件实际上都存在着内电阻或者内阻抗，所以理想电路的谐振与真实发生谐振存在着一定偏差。实际的 LC 谐振电路当中，电容的高频损耗电阻较小，可以忽略；而电感的高频损耗电阻较大，不可以忽视，分析电路时需要将其纳入考量。接下来通过下图所示的电路，说明 RLC 串联电路的工作原理：

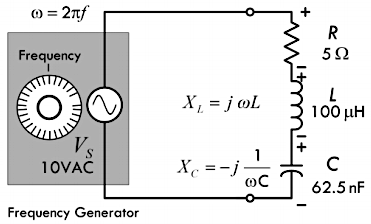
首先，求解出上述 RLC 串联电路的总阻抗 \(Z_{total}\)：

\[ Z_{total} = R + X_L + X_C = R + j \omega L - j \frac{1}{\omega C} = R + j \bigg( \omega L - \frac{1}{\omega C} \bigg) \]

这里依然把上述结果转换为极坐标形式：

\[ Z_{total} = \sqrt{R^2 + (\omega L - \frac{1}{\omega C})^2} \angle \tan^{-1} \bigg( \frac{\omega L - \frac{1}{\omega C}}{R} \bigg) \]

如果不考虑相位，那么流过总阻抗的电流 \(I\) 等于：

\[ I = \frac{V_S}{Z_{total}} = \frac{10 VAC}{\sqrt{R^2 + \big( \omega L - \frac{1}{\omega C} \big)^2}} \]

将电感 \(L = 100 \mu H\)、电容 \(C = 62.5 nF\)、角频率 \(\omega = 2 \pi f\) 代入，既可以求解得到一个关于电流的频率函数：

\[ I = \frac{10 VAC}{\sqrt{25 + (6.28 \times 10^{-4} f - \frac{2546479}{f})^2}} Ω \]

当上述方程里的频率 \(f\) 等于谐振频率 \(f_0 = \frac{1}{2\pi \sqrt{LC}} = \frac{1}{2\pi \sqrt{(100 \times 10^{-6}H)(62.5 \times 10^{-9}F)}} = 63663 Hz\) 的时候，该 LCR 串联谐振电路的总电流 \(I = \frac{V_S}{R} = \frac{10 VAC}{5Ω} = 2A\) 并不会趋于无穷大，而是在发生谐振时感抗与容抗相互抵消，其中电阻可以防止出现阻抗为零的情况。

空载品质因数 \(Q_u\) 就是指电路发生谐振时的电抗除以电阻：

\[ Q_u = \frac{1}{R} \times \sqrt{\frac{L}{C}} \times \frac{X_{L, 0}}{R} = \frac{\omega_0 L}{R} = \frac{2 \pi f_0 L}{R} = \frac{40Ω}{5Ω} = 8 \]

当电路发生谐振的时候，感抗与容抗相互抵消，整个电路的阻抗仅由电阻来决定。由此可以推断，发生谐振时的电流与电压同相，类似于只存在一个电阻的正弦电路。如果当前没有发生谐振，由于感抗或者容抗的增加，总阻抗将会增大。如果当前电路的频率低于谐振频率，那么容抗占据主导地位（电容对于电流的阻碍作用增强）。如果当前电路的频率高于谐振频率，则感抗占据主导地位（电感对于电流的阻碍作用增强）。当电路没有发生谐振的时候，电阻对于电流幅值的影响微不足道。

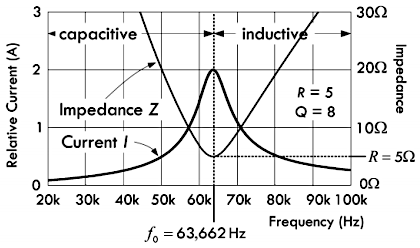
上图当中的电流曲线存在着一个尖锋，当感抗或者容抗与电阻的大小相当时，如果远离谐振频率，那么电流就会缓慢下降，此时电流曲线的尖峰较宽。相反的，当感抗或者容抗比电阻更大时，无论朝哪个方向远离谐振频率，电流都会迅速的下降，此时的电流曲线尖峰较窄。窄带谐振电路对于谐振频率的响应，要比接近谐振频率位置附近的频率响应更大，而宽带谐振电路对于谐振频率附近的频率响应基本都相同。

因此，窄带谐振电路具有更好的选择性，可以表现出对于指定频率信号较强的响应能力（幅值），并且能够抑制其它频率的信号。而宽带谐振电路可以应用于需要对频带内所有信号进行相同响应的场景（而并非只对单一频率有较强响应）。

注意：接下来所要讨论的品质因数与带宽，是体现 RLC 谐振电路频率选择性的两个重要参数。

品质因数

之前内容当中有介绍过，品质因数 Q 是电抗（储能）与电阻（耗能）的比值，在 RLC 串联电路（其中的 R 是元件内阻）当中，电感器 L 的内阻损耗在高频情况下占据主导地位，这意味着电感的 Q 值在很大程度上决定了谐振电路的 Q 值。因为 Q 值与接收功率的外部负载无关，所以这里更改了谐振电路的 Q 值，称其为电路的无负载 \(Q\) 值，并且记作 \(Q_u\)。

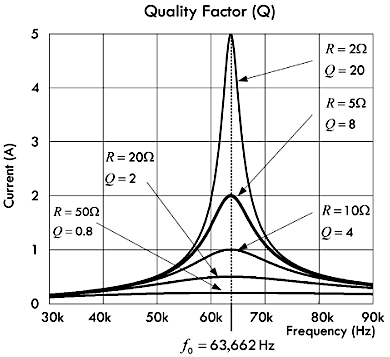
使用上面 RLC 串联谐振电路当中的电阻，除以感抗或者容抗（谐振时的感抗与容抗相等）就可以确定该电路的无负载 Q 值：

\[ Q_u = \frac{X_{L,0}}{R} = \frac{40Ω}{5Ω} = 8 \ 或者\ Q_u = \frac{X_{C,0}}{R} = \frac{40Ω}{5Ω} = 8 \]

上述等式表明，如果增大电阻 R，那么无负载 Q 值 \(Q_u\) 就会降低，谐振电路的响应曲线就会变宽。例如当电阻分别为 10 Ω、20 Ω、50 Ω 时，\(Q_u\) 分别会降低至 4、2、0.8。相反的，如果减小电阻 R，那么无负载 Q 值 \(Q_u\) 就会增大，谐振电路的响应曲线就会变窄。例如当电阻减小至 2Ω 的时候，\(Q_u\) 就会增大到 20。

带宽

除了品质因数 Q 之外，带宽是另外一个用于表征 RLC 谐振电路频率选择特性的物理量。把上面的品质因数曲线图转换为下面的带宽曲线图，即将竖轴的电流更换为相对电流，并将用于表示变化 Q 值的曲线簇向上移动，使得所有曲线都具有相同的峰值电流。通过假设每一条曲线的峰值电流相等，可以非常容易的比较出不同 Q 值时，电流的变化率以及相关的电抗与电阻之比。

从上面的曲线可以看出，与 Q 值较高的电路相比，Q 值较低的电路可以通过更大带宽的频率。带宽被定义为两个频率之间的差值，此时两个频率点上的电流幅值为最大值的 0.707 倍或者 \(\frac{1}{\sqrt{2}}\) 倍。由于电阻消耗的功率与电流的平方成正比，假设这里 R 为常数，则电路在这两个频率点位置的功率，是发生谐振时最大功率的一半。在上面的曲线图当中，已经标识出了这个半功率点，或者称为 -3dB 点。

由于 Q 值大于 10 的曲线近乎完全对称，因而可以很容易的得出带宽（\(WB\)）的计算公式（带宽与频率的单位都是赫兹 Hz）：

\[ 带宽\ BW = \frac{谐振频率\ f_0}{无负载品质因数\ Q_u} \]

例如对于本小节开头的 RLC 串联谐振电路，其在 100KHz 频率时的带宽为 \(BW_1 = \frac{f_0}{Q_u} = \frac{100000 Hz}{8} = 12500Hz\)，而在 1MHz 频率时的带宽为 \(BW_1 = \frac{f_0}{Q_u} = \frac{1000000 Hz}{8} = 125000Hz\)：

RLC 谐振电路元件电压

RLC 谐振电路当中，电感与电容两端的电压可以根据交流欧姆定律求解得到：

\[ \begin{cases} 电容电压\ V_C = X_C \times I = \frac{1}{2 \pi f C} \times I \\ 电感电压\ V_L = X_L \times I = 2 \pi f L \times I \end{cases} \]

因为电感器与电容器会将其储存的能量返还给电路，所以电感器与电容器两端的电压可能会大于电源电压，特别是对于具备高 Q 值的电路，更是尤为如此。

例如在发生谐振时，本小节开头所示 RLC 串联电路里的电容与电感两端电压 \(V_C\) 与 \(V_L\) 分别为:

\[ \begin{cases} V_C = X_C \times I = (40Ω \angle -90°) \times (2A \angle 0°) = 80° VAC \angle -90° \\ V_L = X_L \times I = (40Ω \angle +90°) \times (2A \angle 0°) = 80° VAC \angle +90° \end{cases} \]

将 RMS 值乘以 1.414 就可以将其转换为峰值，即约等于 113V。这样高 Q 值的电路经常出现在天线耦合器当中，由于其功率较大，因而可以承受较高无功电压造成的电弧（无功电压是由电抗元件在线路上产生的变化电压）。即使电源电压处于元件的额定电压范围以内，但是在考虑 Q 值大于 10 的情况时，RLC 串联电路发生谐振时的无功电压 \(V_X\) 可以采用下面公式获得：

\[ 无功电压 V_X = 无负载品质因数 \ Q_u \times 电源电压\ V_S \]

电容损耗

对于频率低于 30 MHz 的串联谐振电路，电容的能量损耗比电感更小。但是在 30 MHz ~ 300 MHz 范围以内，电容的损耗可能会影响到电路的 Q 值。电容损耗主要来自于电容器极板之间电介质的泄漏电阻，其与电感器的内阻损耗存在着区别：电感器的导线损耗电阻与感抗形成串联关系，而电容器的泄漏电阻与容抗形成并联关系。如果电容器的泄漏电阻影响到串联谐振电路的 Q 值，则必须将这个并联的泄漏电阻，转换为串联的等效电阻，其计算公式如下所示：

\[ 串联等效电阻\ R_S = \frac{容抗\ X_C^2}{泄露电阻\ R_P} = \frac{1}{R_P \times (2 \pi f C)^2} \]

注意：把该串联等效电阻与电感的导线损耗电阻相加，就可以得到 RLC 谐振电路当中电阻 \(R\) 的取值（该书将 RLC 电路中的电阻 R 视为电感 L 与电容 C 的内阻之和 ）。

▶【例题】10.0pF 的电容器在 40.0 MHz 频率时的泄漏电阻为 9000 Ω，求解其等效串联电阻 \(R_S\) ?

◉【解】根据题设条件，该电路的等效串联电阻 \(R_S\) 等于：

\[ R_S = \frac{1}{R_P \times (2 \pi f C)^2} = \frac{1}{9000Ω \times (6.283 \times 40.0 \times 10^6 \times 10.0 \times 10^{-12})^2} = 17.6 Ω \]

注意：计算串联谐振电路的阻抗、电流、带宽时，需要把串联泄漏电阻与电感线圈内电阻相加，但是由于集肤效应的存在，电感的内阻会随着频率的提高而增大，从而导致电容与电感的全部损耗，严重降低了电路的 Q 值。

▶【例题】假设一个串联谐振电路的损耗电阻为 4Ω，求解感抗与容抗都为 200Ω 时电路的无负载 Q 值 ？以及感抗与容抗为 20Ω 时候的无负载 Q 值 ？

◉【解】感抗与容抗都为 200Ω 时电路的无负载 Q 值 \(Q_{u1}\) 等于：

\[ Q_{u1} = \frac{X_1}{R} = \frac{200Ω}{4Ω} = 50 \]

◉【解】感抗与容抗都为 20Ω 时电路的无负载 Q 值 \(Q_{u2}\) 等于：

\[ Q_{u2} = \frac{X_2}{R} = \frac{20Ω}{4Ω} = 5 \]

▶【例题】如果一个串联谐振电路的工作频率为 7.75 MHz，工作带宽为 775 kHz，求解该电路的无负载 Q 值 ？

◉【解】根据题设条件，这个电路的无负载 Q 值 \(Q_u\) 等于：

\[ Q_u = \frac{f}{BW} = \frac{7.75MHz}{0.775 MHz} = 10 \]

RLC 并联谐振

下图是一个典型的RLC 并联谐振电路，类似于 RLC 串联谐振电路，电感线圈的内阻是主要的功率损耗源，因而在电感支路侧添加了一个串联电阻。RLC 串联谐振电路的阻抗会在谐振时趋于最小值，而 RLC 并联谐振电路的阻抗则会在谐振时趋于最大值，所以通常称 RLC 并联谐振电路为反谐振电路或者带阻电路（而 RLC 串联谐振电路被称为带通电路）。

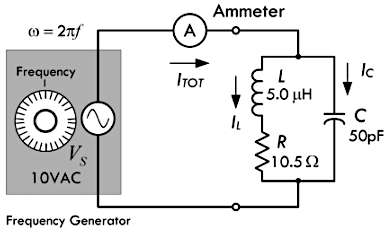
LRC 并联电路的总阻抗 \(Z_{total}\) 等于感抗 \(X_L\) 与电阻 \(R\) 串联，再与容抗 \(X_C\) 进行并联：

\[ Z_{total} = \frac{(R + X_L) \times X_C}{(R + X_L) + X_C} = \frac{(R + j \omega L) \times (- j \frac{1}{\omega C})}{(R + j \omega L) + (- j \frac{1}{\omega C})} = \frac{\frac{L}{C} - j \frac{R}{\omega C}}{R + j (\omega L - \frac{1}{\omega C})} \]

按照惯例，同样将总阻抗 \(Z_{total}\) 转换为极坐标形式：

\[ Z_{total} = \frac {\sqrt{(\frac{L}{C})^2 + (\frac{R}{\omega C})^2} \angle \tan^{-1} \big[\frac{R/(\omega C)}{L/C} \big] } {\sqrt{R^2 + (\omega L - \frac{1}{\omega C})^2} \angle \tan^{-1} \big[ \frac{\omega L - \frac{1}{\omega C}}{R} \big]} \]

将电感 \(L = 5.0µH\)、电容 \(C = 50pF\)、电阻 \(R = 10.5Ω\)、角频率 \(ω = 2 \pi f\) 分别代入，就可以得到忽略相位的总阻抗 \(Z_{total}\)：

\[ Z_{total} = \frac {\sqrt{1.0 \times 10^{10} + \big(\frac{3.34 \times 10^{10}}{f} \big)^2}} {\sqrt{110.3 + \big( 3.14 \times 10^{-5} \times f - \frac{3.18 \times 10^9}{f} \big)^2}}\ Ω \]

进一步的就可以得到一个不考虑相位角的总电流 \(I\)：

\[ I_{total} = \frac{V_S}{Z_{total}} = \frac{10 V}{\frac {\sqrt{1.0 \times 10^{10} + \big(\frac{3.34 \times 10^{10}}{f} \big)^2}} {\sqrt{110.3 + \big( 3.14 \times 10^{-5} \times f - \frac{3.18 \times 10^9}{f} \big)^2}}\ Ω} \]

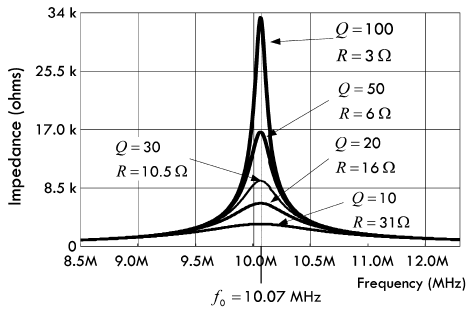
将上面的等式输入电路仿真工具，就可以得到如下的谐振频率特性曲线：

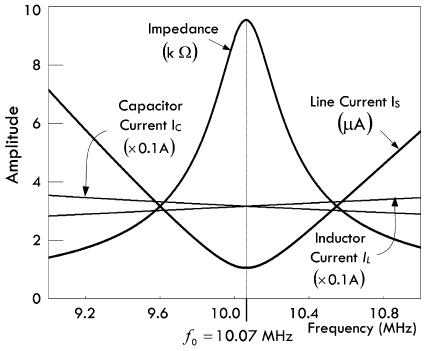
观察上图可以发现，在特定的频率之下，阻抗趋于最大值，总电流趋于最小值。但是这个频率并非位于 \(X_L = X_C\) 的位置，不属于 LC 并联电路或者 RLC 串联电路的谐振频率点。RLC 并联电路的谐振频率表达式较为复杂，总共存在着三种表达方式，在这里我们采用 LC 并联电路来近似的进行表示：

\[ f_0 = \frac{1}{2 \pi \sqrt{LC}} = 10,070,000 Hz = 10.07 MHz \]

利用电感 \(L\) 的感抗，就可以得到无负载 Q 值 \(Q_u\)：

\[ Q_u = \frac{X_{L,0}}{R} = \frac{\omega_0 L}{R} = \frac{2 \pi f_0 L}{R} = \frac{316.4Ω}{10.5Ω} = 30 \]

下图所示的曲线展示了电感支路里的串联电阻大小，对于品质因数 Q 值的影响：

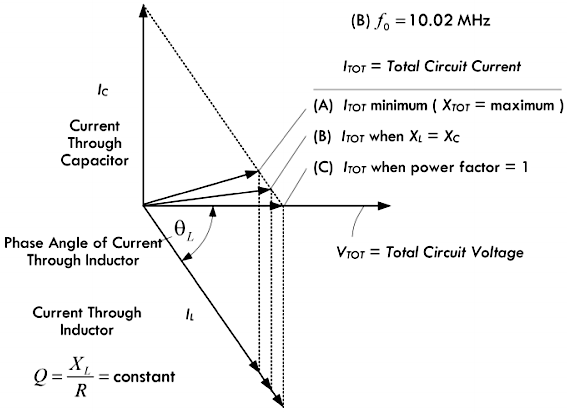
RLC 并联谐振电路里的电阻 \(R\) 改变了电路的谐振条件，例如当感抗 \(X_L\) 与容抗 \(X_C\) 相等时，电感与电容支路的阻抗不为零。由于电阻的存在，使得电感支路的阻抗比电容支路的容抗更大，并且与 \(X_C\) 的相位角不为 180°，因而电路的总电流并非最小值，且电流与电压的相位也不相同，如下图当中的直线 A 所示。

如果稍微调整电感的取值，并且保持 Q 值为常数，就会得到一个可以使得电流达到最小值的频率。我们把电流达到最小值作为 RLC 并联电路发生谐振的标志，电流最小值（或者阻抗最大值）所在的频率点称为反谐振点。注意不要把反谐振点与条件 \(X_L = X_C\) 混淆。电感被微调以后，电流与电压的相位会稍有不同，如下图中的直线 B 所示。

当电路的 Q 值达到 10 以上时，谐振点之间的差异很小，几乎都集中在同一个频率，这种情况下可以采取近似计算，认为最小电流与电压之间的相位几乎相同，从而避免复杂的计算过程。如果假设电路的 Q 值大于 10，那么可以去掉电感支路上的串联电阻，改为采用一个并联电阻来等效电感的内阻：

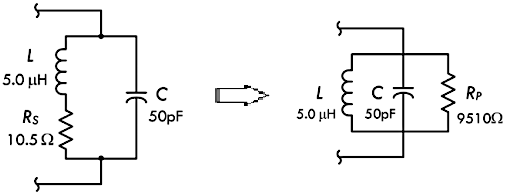
上图左侧的串联电阻 \(R_S\) 被右侧等效电路当中的并联电阻 \(R_P\) 替代，反之亦然。通常称这个并联等效电阻为并联谐振电路的动态电阻，其取值与电感支路的串联电阻成反比。换而言之，并联等效电阻会随着电路 Q 值的增加而变大，并联等效电阻 \(R_P\) 的近似计算公式如下面所示：

\[ R_P = \frac{X_L^2}{R_S} = \frac{(2 \pi f L)^2}{R_S} = Q_u X_L \]

▶【例题】假设上图左侧电路发生谐振时的感抗为 316Ω，串联电阻为 10.5Ω，求解电感的并联等效电阻，以及无负载 Q 值 ？

◉【解】根据题设条件，可以得到电感的并联等效电阻 \(R_P\) 为：

\[ R_P = \frac{X_L^2}{R_S} = \frac{(316Ω)^2}{10.5Ω} = 9510Ω \]

◉【解】电感线圈的无负载 Q 值 \(Q_u\) 等于电感的感抗 \(X_L\) 除以其串联电阻 \(R_S\)（内阻）：

\[ Q_u = \frac{X_L}{R_S} = \frac{316Ω}{10.5Ω} = 30 \]

注意：让 \(Q_u\) 乘以电抗，也可以得到与电感器串联电阻近似的并联等效电阻 \(R_P\)。

发生谐振的时候，假设并联等效电路满足关系式 \(X_L = X_C\)，则 \(R_P\) 为该并联谐振电路的等效阻抗。由于感抗与容抗相等，则电压与电流保持同相。换而言之，发生谐振时电路只呈现并联电阻的特性，因此前述的并联等效电阻 \(R_P\) 近似计算公式，可以重新改写为下面的形式：

\[ Z = \frac{X_L^2}{R_S} = \frac{(2 \pi f L)^2}{R_S} = Q_u X_L \]

当电路的频率小于谐振频率时，感抗小于容抗，此时经过电感的电流比经过电容的电流更大，相互之间仅有一部分被抵消掉，因而总电流大于电阻的电流。当频率大于谐振频率时，则情况正好相反，经过电容的电流比经过电感的电流更大，总电流仍然大于电阻的电流。而在发生谐振时，电流完全由并联等效电阻 \(R_P\) 决定，如果 \(R_P\) 增大电流就会减小，如果 \(R_P\) 减小电流就会增大。

随着总电流在谐振之后增大，并联谐振电路的阻抗下降，电压与电流之间的相位差增大，阻抗下降的速率是 \(Q_u\) 的函数。本节内容开始位置的曲线簇，就展示了电路的 Q 值在 \(10 \sim 100\) 范围内，阻抗由于发生谐振而下降的情况。并联电路阻抗的曲线簇本质上与串联电路电流的曲线簇相同。

如果应用半功率（-3dB）点来比较和测试电路性能，那么就可以将串联谐振电路的带宽公式 \(BW = \frac{f}{Q_u}\) 应用到并联谐振电路当中。接下来的表格，对于并联谐振电路的性能特点进行了归纳总结：

高 Q 值与低 Q 值的并联谐振电路比较：

	高 Q 值	低 Q 值
选择性	高	低
带宽	窄	宽
阻抗	高	低
线路电流	小	大
环流	大	小

当电感 L 和电容 C 分别为常数时，电路远离谐振点之后的特性：

	高于谐振频率	低于谐振频率
感抗	增大	减小
容抗	减小	增大
电路电阻	不变	不变
电路阻抗	减小	减小
线路电流	增大	增大
环流	减小	减小
电路特性	容性	感性

循环电流

已知理想 LC 并联谐振电路发生谐振时，电容与电感之间会存在比较大的循环电流，而电源端输出的电流为零。对于实际的 RLC 并联谐振电路，发生谐振时同样会存在循环电流，这个电流会比电源输出的电流更大（电源由于负载的存在电流较小，但是不会为零）。这是由于尽管谐振时电路的阻抗较大，但并非是无穷大，循环电流在通过电感与电容时产生损耗，而大部分损耗是由电感的内阻所造成。实际的 RLC 并联谐振电路（下图左）及其等效电路（下图右）如下图所示：

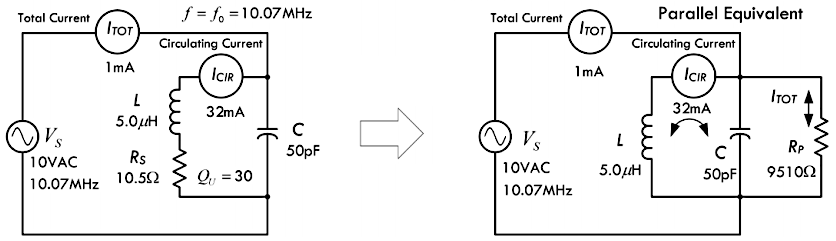
根据上图右侧的并联等效电路，可以分别求解得到电感、电容、电阻上面的电流值 \(I_L\)、\(I_C\)、\(I_R\)：

\[ \begin{aligned} I_R &= \frac{V_S}{R_P} = \frac{10 VAC}{9510Ω} = 1 mA \\ I_L &= \frac{V_S}{X_L} = \frac{V_S}{2 \pi f L} = \frac{10 VAC}{2 \pi \times (10.07 \times 10^6 s^{-1})\times(5.0 \times 10^{-6}H)} = \frac{10 VAC}{316Ω} = 32mA \\ I_C &= \frac{V_S}{X_C} = \frac{V_S}{\frac{1}{2 \pi f C}} = \frac{10 VAC}{\frac{1}{(2 \pi) \times (10.07 \times 10^6 s^{-1}) \times (50.0 \times 10^{-12}F)}} = \frac{10 VAC}{316Ω} = 32 mA \end{aligned} \]

当电路工作于谐振频率时，循环电流 \(I_{circuiting} = I_C = I_L\)，如果并联谐振电路的无负载 Q 值大于 10，那么循环电流可以近似的等于 \(I_{circuiting} = Q_u \times I_{total}\)。在上面的例子当中，总电流 \(I_R = 1 mA\)，电路的 Q 值等于 30，则循环电流 \(I_{circuiting} \approx 30 \times 1mA = 30mA\)。

▶【例题】假设并联谐振电路的总电流为 50mA，Q 值等于 100，求解经过元件的循环电流 ？

◉【解】根据题设条件，可以求解得到该电路当中的循环电流 \(I_C\)：

\[ I_C = Q_u \times I_T = 100 \times 0.05 A = 5 A \]

无负载电路 Q 值

在许多谐振电路的应用当中，实际的功率损耗主要消耗在谐振电路的内阻上面，当频率低于 30MHz 时，这个内阻主要体现为电感器的内电阻。增加电感器的线圈匝数，会让感抗比线圈的内阻增加得更快。高 Q 值电路当中的电感器，通常会具有较大的电感值。

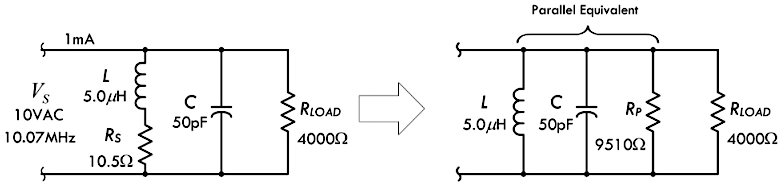
当能量通过谐振电路传递到负载的时候，谐振电路消耗的能量通常会比负载消耗的能量更小。如果负载消耗的能量是电感与电容消耗能量的 10 倍以上，那么相比于负载电阻，谐振电路的并联阻抗将会更大，整个电路的实际阻抗等于负载阻抗。在这种情况下计算 Q 值时，可以使用负载电阻代替电路阻抗，此时并联谐振电路的 Q 值计算公式为：

\[ 带负载电路的 Q 值\ Q_{LOAD} = \frac{并联负载电阻\ R_{LOAD}}{电抗\ X} \]

▶【例题】将一个 4000Ω 电阻负载连接至谐振电路，当电路发生谐振时，感抗和容抗都为 316Ω，试计算该电路的带负载 Q 值 ？

◉【解】根据题设条件，就可以求解得到该电路的带负载 Q 值 \(Q_{LOAD}\)：

\[ Q_{LOAD} = \frac{R_{LOAD}}{X} = \frac{4000Ω}{316Ω} = 13 \]

注意：当电路的电抗下降时，电路的带负载 Q 值就会增加，因而当一个带负载电路的电阻较小（几千欧姆）时，必须使用低电抗值的元件（大电容和小电感），使得发生谐振时的 Q 值更大。

分贝

电子学当中，经常需要比较两个信号的幅值以及功率。例如一个放大器的输出电压为输入电压的 10 倍，此时的比值 \(\frac{V_{out}}{V_{in}} = \frac{10 VAC}{1 VAC} = 10\) 被称为增益；而一个放大器的输出电压小于输入电压有 10 倍，则比值 \(\frac{V_{out}}{V_{in}} = \frac{1 VAC}{10 VAC} = 0.1\) 被称为衰减。

当两个信号的幅值或者功率比值差距较大的时候，绘制曲线将会变成一件非常困难的事情。在电子学当中，就通过贝尔这个单位引入特殊的对数坐标解决这个问题，贝尔 \(bel\) 是指比较功率 \(P_1\) 与参考功率 \(P_0\) 的比值：

\[ 贝尔\ bel = \log \bigg(\frac{比较功率\ P_1}{参考功率\ P_0}\bigg) \]

电子学当中，贝尔 \(bel\) 经常用于比较功率的大小，但是应用更为普遍的单位是分贝 dB：

\[ 1 分贝dB = \frac{1}{10} 贝尔bel \implies 1 贝尔bel = 10 分贝dB \]

因而在这里，可以改用分贝来度量功率的大小，前面的公式需要改写为下面的形式：

\[ 分贝\ dB = 10 \times \log \bigg(\frac{比较功率\ P_1}{参考功率\ P_0}\bigg) \]

▶【例题】如果一个放大器的输入信号功率为 1W，而输出信号功率达到 50W，试求解该放大器的增益 ？

◉【解】根据题设条件，可以求解出该放大器的增益为 \(17dB\)：

\[ dB = 10 \times \log \bigg( \frac{50W}{1W} \bigg) = 10 \times \log (50) = 17 dB \]

比较电路当中的信号大小时，通常已知的是信号的电压或者电流，而并不是功率。虽然可以通过电路的阻抗计算出功率，但是更为简单的办法是将交流欧姆定律代入分贝表达式中的功率，此处调用 \(P = \frac{V^2}{Z} = \frac{I^2}{Z}\)（只有当电路的阻抗不随电压或电流的变化而波动时，这种情况才会成立），即只要阻抗保持不变，就可以用分贝来比较电压与电流信号。

\[ \begin{cases} dB = 10 \log \bigg( \frac{V_1^2}{V_0^2} \bigg) = 20 \log \bigg( \frac{V_1}{V_0} \bigg) \\ dB = 10 \log \bigg( \frac{I_1^2}{I_0^2} \bigg) = 20 \log \bigg( \frac{I_1}{I_0} \bigg) \end{cases} \]

如果输出功率是输入功率的两倍，那么就是增益 3.01 dB：

\[ dB = 10 \log(2) = 3.01 dB \]

如果输出功率是输入功率的一半，那么就是衰减 -3.01 dB：

\[ dB = 10 \log(0.5) = -3.01 dB \]

注意：通常会省略小数点后面的 0.01，即认为功率翻倍时的增益为 \(3dB\)，而在功率减半时的衰减为 \(-3dB\)。

下面的表格展示了常见的分贝值，和对应的功率变化情况，以及电压与电流的变化情况：

注意：只有当对应的阻抗相等时，上面表格当中所列出的关系才会成立。

我们将以分贝作为单位的值，与 1mW 功率的比值称为分贝毫瓦 dBm。这是一个用于指代功率的绝对值（分贝是一个表示功率的相对值）。例如从天线传递到接收设备的信号功率为 \(2 \times 10^{-13} mW\)，此时接收设备的信号输入强度则可以表示为：

\[ dB_m = 10 \times \log \bigg( \frac{2 \times 10^{-13} mW}{1mW} \bigg) = -127 dBm \]

除此之外，还可以将使用分贝作为单位的值，与 1W 功率的比值称为分贝瓦 dBW，而与 1V 电压幅值的比值称为分贝伏 dBV，它们各自都拥有着相应的物理意义与用途。