闭环控制算法 PID 的原理剖析与实现

比例-积分-微分（PID，Proportion Integration Differentiation）是一种广泛运用于自动化控制领域的经典算法，属于众多控制算法当中最能够体现反馈思想的算法。该算法由 Nicolas Minorsky 于 1922 年船舶舵机控制理论的研究当中提出，随后以其卓越的性能和易于实现的特性，在 温度控制、电机调速、过程控制 等诸多领域逐渐普及。无论是简单的单变量系统，还是复杂的多变量系统，PID 控制算法都能通过调节 比例、积分、微分 三个参数实现精准的控制。

例如把一台无刷电机连接到额定输出电压为 12V 的锂电池组，然后通过一个占空比为 50% 的 PWM 波进行驱动，刚开始的时候电机运行速度很快且扭矩充足，但是随着时间的流逝，锂电池的放电电压逐步下降，开始影响到电机的转速和转矩。如果这块锂电池组刚充满的时候，输出电压为 12V，PWM 波占空比为 50%，那么作用在电机两端的等效电压为 \(12V \times 50\% = 6V\)。放电持续一段时间之后，锂电池电压降低至 9V，此时电机两端的等效电压也会降低到 \(9V \times 50\% = 4.5V\)，电机的转速和转矩开始出现明显的下降。如果需要在锂电池的整个放电周期当中，保持电机 转速 和 转矩 的稳定，就有必要引入这里将要介绍的 PID 控制理论。

控制系统分类

在众多工业自动化控制算法当中，通常会根据当前是否存在有反馈信号，而将其笼统的划分为开环控制和闭环控制两种类型：

• 开环控制系统（Open Loop）：被控对象的输出(即被控制量)不会影响到控制装置的输出，这种控制系统不需要返回被控量，也不会形成任何的闭环回路。
• 闭环控制系统（Closed Loop）：被控对象的输出（通过检测装置）返回并影响到控制装置的输出，进而形成闭环的控制回路。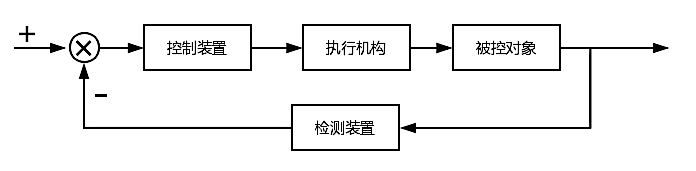

注意：根据反馈信号与控制信号的极性是否相同，还可以将闭环控制系统进一步划分为正反馈和负反馈两种类型。

PID 算法属于一种闭环控制系统，下图展示了使用 PID 控制器对直流无刷电机进行调速的过程，无刷电机的目标转速 \(n_0(t)\) 将会与实际转速 \(n(t)\) 进行比较，其差值 \(e(t)=n_0(t)-n(t)\) 经过 PID 控制器调整之后，输出的电压控制信号 \(u(t)\) 经过功率放大器处理之后，就可以驱动直流电机并实时调整其 转速 与 转矩：

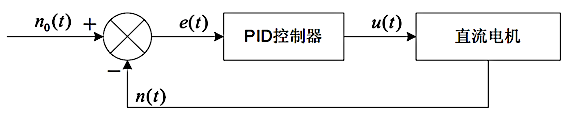
PID 算法概览

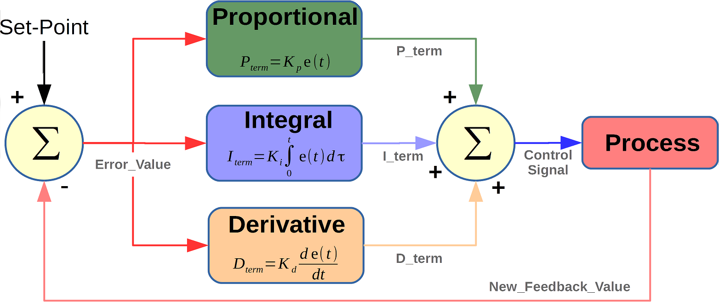
PID 是比例（Proportional [prəˈpɔːʃən(ə)l]）、积分（Integral [ˈɪntɪɡrəl]）、微分（Differential [ˌdɪfəˈrenʃ(ə)l]）三个英文单词的首字母缩写。顾名思义，这是一种基于系统运行时产生的 偏差，利用比例、积分、微分计算出实际控制量的一种算法。在下面的示意图当中，展示了 PID 算法的基本工作流程，其中的 \(r(t)\) 是设定的目标值，\(y(t)\) 是实际的输出值：

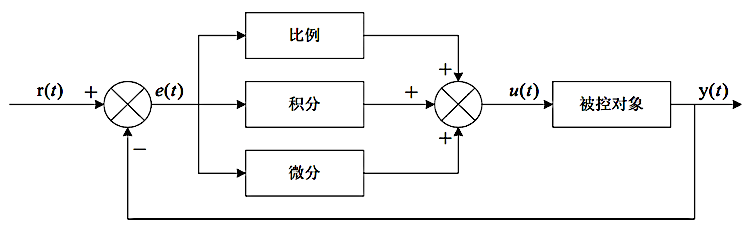
将设定的目标值 \(r(t)\) 与实际输出值 \(y(t)\) 相减，就可以计算得到偏差 \(e(t)\) 的值：

\[ e(t) = r(t) - y(t) \]

上面示意图当中的偏差 \(e(t)\) 将会作为 PID 控制器的输入，而电压控制信号 \(u(t)\) 则会作为 PID 控制器的输出或者被控对象的输入，整个 PID 控制器的算法可以被整理为如下的离散公式（PID 算法的连续公式不利于计算机处理，这里不作介绍）：

\[ \begin{align} u(t) & = \Biggl( K_p \times e(t) \Biggl) + \Biggl( K_i \times \int^t_0 e(t) dt \Biggl) + \Biggl( K_d \times \frac{de(t)}{dt} \Biggl) \\ & = K_p \Biggl( e(t) + \frac{1}{T_i} \int^t_0 e(t) dt + T_d \frac{de(t)}{dt} \Biggl) \end{align} \]

上述第 1 个公式中的参数 \(K_p\)、\(K_i\)、\(K_d\) 分别是 PID 控制器的比例系数、积分系数、微分系数。而第 2 个公式中的 \(T_i\) 是积分时间、\(T_d\) 则是微分时间。基于上面这个公式，就可以把 PID 算法的控制流程梳理为如下三个步骤：

1. 首先，计算出 设定目标值 与 实际输出值 之间的偏差。
2. 然后，将结果导入 比例、积分、微分 三个 PID 算法控制环节进行处理。
3. 最后，通过闭环控制系统，不断的将 实际输出值 反馈至偏差计算阶段，如此循环往复。

根据上述 PID 算法的理论公式，可以将其划分为 比例、积分、微分 三个控制环节，在接下来内容里我们会分别进行讨论。

注意：实际的工业控制系统当中，并非需要 PID 的全部三个环节都参与控制，有些控制场景下只需要比例环节或者积分环节就可以控制。除此之外，每一套控制系统的 PID 系数并不是通用的，需要根据实际情况进行标定。

比例 Proportional

比例控制环节主要用于补偿目标值与实际值之间的偏差，如果产生偏差 PID 控制器将会立刻产生控制作用，使得控制量向着降低偏差的方向进行变化，比例控制环节的数学式表达如下所示：

\[ 比例系数 K_p \times 偏差 e(t) \]

观察上面的数学公式可以发现，比例控制作用的强弱，主要取决于比例系数 \(K_p\)，该参数的取值具有如下特点：

• 优点：比例系数越大，控制作用就会越强，过渡过程就会越快，控制过程的静态偏差也就会越小；
• 缺点：比例系数越大，也就越容易让控制信号发生振荡，从而破坏整个控制系统的稳定性；

因此，必须选用合适的比例系数取值，才能够减少过渡时间，降低振荡发生的概率，进而降低静态偏差，确保整个控制系统的稳定工作。

积分 Integral

积分控制环节主要用于消除在比例控制环节产生的静态偏差（即控制系统达到稳态之后，输出值与期望值之间的偏差），其数学式表达如下所示：

\[ 比例系数 K_p \times \frac{1}{积分时间 T_i} \times \int^t_0 偏差 e(t) dt \]

观察上面的数学表达式可知：只要存在着偏差，其控制作用就会不断的增强。只有当偏差 \(e(t)=0\) 的时候，其控制作用才会变成一个常数。虽然积分控制环节可以消除静态误差，但是同时也会降低控制系统的响应速度，导致控制系统出现超调（即输出量在达到设定值之前，就已经超过设定值的现象），所以必须根据实际的控制要求来选定积分时间 \(T_i\) 的取值：

• 积分常数 \(T_i\) 越大，积分的累积作用就会越弱。虽然控制系统在过渡过程当中不会发生振荡，但是会减缓消除静态偏差的过程。但是可以降低超调量，提高控制系统的稳定性；
• 积分常数 \(T_i\) 越小，积分的累积作用就会越强，此时过渡过程当中可能会产生振荡，不过消除静态偏差所需的时间比较短。

微分 Differential

微分控制环节用于根据偏差的变化趋势或者变化速度，在偏差来临之前引入一个修正信号，从而将偏差消灭在萌芽状态，进而降低控制系统的动态偏差（即控制系统输出与期望值之间的差异随着时间变化的情况），微分控制环节的数学表达式如下所示：

\[ 比例系数 K_p \times 微分时间 T_d \times \frac{de(t)}{dt} \]

观察上述公式可以发现，其控制作用主要由微分时间 \(T_d\) 来决定。如果 \(T_d\) 的值越大，控制系统抑制偏差 \(e(t)\) 变化的能力就会越强。反之如果 \(T_d\) 越小，其抑制偏差 \(e(t)\) 变化的能力就会越弱，因此该参数同样需要合理的进行取值。

概而言之，PID 控制系统不但需要在比例控制环节对 偏差量 做出响应，以及在积分控制环节消除 静态误差 之外，还需要在微分控制环节根据偏差的变化趋势，预先修正动态偏差。

• 优点：微分控制环节有助于避免控制系统出现超调和发生振荡，同时能够提高控制系统的响应速度，并且改善动态性能；
• 缺点：容易引入高频噪声，在干扰信号比较严重的闭环控制系统当中，需要慎重引入微分控制环节，以及选择合理的微分时间 \(T_d\)；

PID 算法的直观示例

本章节内容，通过一个【阀门向水箱注水】的形象实例来说明 PID 算法理论的基本思想，假设现在有下图这样一个透明的水箱，水位高度可以进行实时的观测，现在要通过顶部的阀门向水箱从零开始注水，以达到某个确定的水位（例如 100% 完全注满）：

比例调节阶段

如果想将水箱里的水灌注到指定位置，那么只需要观测水位实际位置与目标位置的差值即可。如果差值较大，就将阀门开大一些。如果差值较小，就将阀门关小一些；伴随水位差值越来越小，直至完全关闭阀门，从而达到将水灌注到指定水位的目的。这种场景，就属于 PID 控制算法的比例控制环节，输出水量 \(u(t)\) 等于比例系数 \(K_p\) 与水位差 \(e(t)\) 的乘积：

\[ 输出 u(t) = 比例系数 K_p \times 偏差 e(t) \]

这里的比例系数 \(K_p\) 就相当于阀门的开关幅度，该值越大就说明阀门开启得比较大，阀门的出水量就会越大，水箱里水量的调节速度就会更快；该值越小则说明阀门开启得比较小，阀门出水量和水箱水位的调节速度都会降低。换而言之，总体展现的就是通过增大比例系数，从而提高控制系统响应的思想。

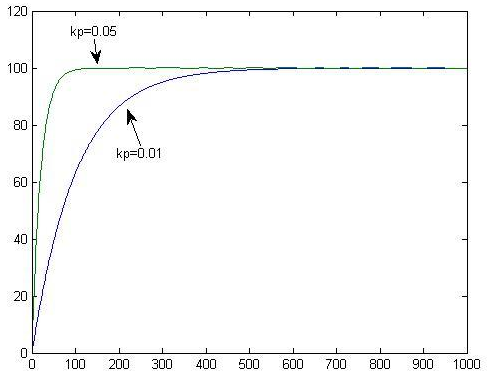
例如在上面的示意图当中，比例系数 \(K_p = 0.05\) 时的控制输出，将会比 \(K_p = 0.01\) 的输出要更快的达到 100% 的稳态。

积分调节阶段

如果此时添加了一个用于放水的阀门，当放水速度等于注水速度的时候，此时的偏差 \(e(t) = 0\)。相应的当 \(e(t) \neq 0\) 的时候，水位的高度就会始终存在着一个静态误差。如果此时放水速度并非一个恒定不变的常量，那么单纯按比例进行控制，就无法补足这个静态不变的误差。因而必须引入积分控制环节，依靠动态的调整注水量来解决这个问题，此时的控制算法会扩展为如下的方程式：

\[ 输出 u(t) = \Biggl( 比例系数 K_p \times 偏差 e(t) \Biggl) + \Biggl( \frac{比例系数 K_p}{积分时间 T_i} \times \int^t_0 e(t) dt \Biggl) \]

积分控制环节存在着一个重要的参数积分系数 \(K_i = \frac{比例系数 K_p}{积分时间 T_i}\)，积分时间用于累计过程误差，累计的误差越大，调节的力度就会越大。在水箱注水的例子里，可以理解为在第 1 个注水阀门之外，额外又增加了第 2 个注水阀门。这个阀门的工作规则是：当水位低于目标高度时，就持续加大阀门开启力度。当水位高于目标高度时，就不断减少阀门开启力度。这个时候，如果水箱的放水量和放水速度不发生变化，那么在经过若干次的调整之后，就可以消除控制系统的静态误差。换而言之，积分环节可以消除控制系统的静态误差。

积分系数 \(K_i\) 越大，在比例系数 \(K_p\) 为定值的前提下，就必须选用较小的积分时间 \(T_i\) 取值，此时相当于降低了积分调节的灵敏度。如果当前没有达到预定水位，那么第 2 个阀门就会持续向水箱进行注水。当达到目标水位的时候，这个阀门也就达到了最大的出水量，进而开始导致水箱的注水量发生溢出，这部分溢出的注水量就被称作超调。因此第 2 个阀门的开启幅度越大，其达到目标水位的速度也就会越快，但是由于超调而导致的震荡也就会越多。观察上面的示意图， 可以发现虽然增大积分时间 \(T_i\) 有助于降低控制信号的超调，提升控制系统的稳定性，但是同时也会带来静态偏差消除时间过久的问题。

微分调节阶段

如果放水阀门的出水量并非一个稳定的常数，而是一个在不断发生变化的变量。那么积分调节阶段所引入的第 2 个阀门，依然在根据原先设定的目标水位进行控制的话，由于很难知晓下一时刻的出水量大小，调整操作往往就会显得滞后。此时仅仅只依靠比例和积分调节就不那么奏效，必须再行引入一个新的微分调节阶段的公式：

\[ u(t) = \Biggl( K_p \times e(t) \Biggl) + \Biggl( \frac{K_p}{T_i} \int^t_0 e(t) dt \Biggl) + \Biggl( K_p \times T_d \frac{de(t)}{dt} \Biggl) \]

微分调节阶段相当于再次在水箱上添加第 3 个注水阀门，以及第 2 个放水阀门，从而一边持续的观测水位变化，另一边不断的进行放水和注水，根据水位实际高度与预期高度差值的变化率来调整阀门的状态，从而达到更佳的水位控制效果。

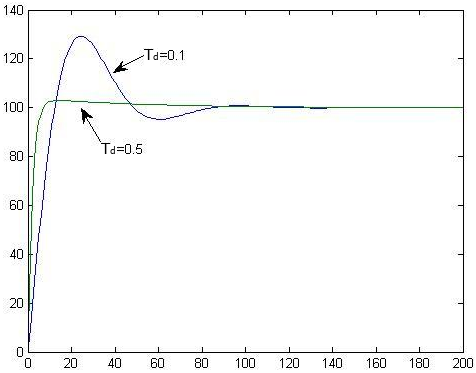
微分控制环节的重要参数是微分系数 \(K_d = 比例系数 K_p \times 微分时间 T_d\)，当比例系数 \(K_p\) 的取值一定的情况下，微分调节阶段的控制作用主要由微分时间 \(T_d\) 来决定，其值越大，控制系统抑制动态偏差的能力就越强，反之其值越小，控制系统抑制动态偏差的能力就会越弱。

注意：本质上而言，积分控制环节调节的是整个注入和放水过程的静态偏差，而微分控制环节调节的则是整个过程的动态偏差。

位置式 PID 算法

由于常用的 MCU 微控制器作为一种数字芯片，只能根据采样时刻的偏差计算控制量，而不能像模拟量那样进行连续的采样与控制，因而下面 PID 公式中的 积分项 与 微分项 无法直接使用，必须进行离散化处理：

\[ \begin{align} u(t) = K_p \Biggl( e(t) + \frac{1}{T_i} \int^t_0 e(t) dt + T_d \frac{de(t)}{dt} \Biggl) \end{align} \]

首先将 T 作为采样周期，k 作为采样序号，然后用离散的采样时间 kT 对应连续的时间 t，然后就会得到如下一系列近似的变换：

\[ \begin{cases} t \thickapprox k \cdot T，其中 \Big(k = 0,1,2,3...\Big) \\ \Biggl( \int^t_0 e(t)dt \Biggl) \thickapprox \Biggl( T \sum^k_{j=0} e(jT) \Biggl) = \Biggl( T \sum^k_{j=0} ej \Biggl) \\ \Biggl (\frac{de(t)}{dt} \Biggl) = \Biggl( \frac{e(kT) - e[kT-T]}{T} \Biggl) = \Biggl(\frac{e_k - e_{k-1}}{T} \Biggl) \end{cases} \]

将这些近似的变换代入到前面的 PID 算法公式，并且将 \(e(kT)\) 简化为 \(e_k\)，就可以得到 PID 算法的离散表达公式：

\[ \begin{align} u_k & = \Biggl( K_p \times e_k \Biggl) + \Biggl( K_i \times \sum^k_{j=0} e_j\Biggl) + \Biggl[ K_d \times (e_k - e_{k-1}) \Biggl] \\ & = K_p \times \Biggl[ e_k + \frac{T}{T_i} \times \sum^k_{j=0} e_j + T_d \times \frac{(e_k - e_{k-1})}{T} \Biggl] \end{align} \]

接下来的表格里，对于上述 PID 离散公式当中变量的作用，分别进行了解释和说明。观察可以发现上述公式基本给出了全部控制量，因而也被称作全量式 PID 控制算法，或者位置式 PID 控制算法：

PID 离散公式中的变量	参数说明
\(k\)	采样序号，取值范围为 \(k = 0,1,2,...\)
\(u_k\)	第 \(k\) 次采样时刻，PID 控制器的输出值
\(e_k\)	第 \(k\) 次采样时刻，输入到 PID 控制器的偏差值
\(e_k\)	第 \(k - 1\) 次采样时刻，输入到 PID 控制器的偏差值
\(K_i\)	积分系数，\(K_i= K_p \times \frac{T}{T_i}\)
\(K_d\)	微分系数，\(K_d= K_p \times \frac{T_d}{T}\)

这里把位置式 PID 控制算法的优缺点，分别总结为下面的列表：

• 优点：如果 PID 控制系统反馈回路的采样周期足够小，那么通过这种位置式 PID 控制算法就可以近似的计算出控制量，在这个离散控制过程当中获得的效果，会与连续控制过程产生的效果非常之接近。
• 缺点：每次全量输出都会与过去的状态有关，需要对 \(e_k\) 进行累加，计算任务较为繁重；如果 PID 控制器出现故障，可能会导致输出的控制量 \(u_k\) 大幅度发生变化（由于输入的是绝对数值），极有可能导致严重的工业生产事故。接下来将要介绍的增量式 PID 算法，就为了解决这个问题而出现的。

增量式 PID 算法

增量式 PID 算法输出的是控制量的增量 \(\Delta U_k\)，相应的 PID 控制器的执行机构运行的也是这个增量，而非像位置式 PID 算法那样输出一个幅度比较大的绝对数值。增量式 PID 控制算法，可以通过前述的如下 PID 离散公式推导得出：

\[ u_k = K_p \times \Biggl[ e(k) + \frac{T}{T_i} \times \sum^k_{j=0} e_j + T_d \times \frac{(e_k - e_{k-1})}{T} \Biggl] \]

根据这个公式，就可以知道 PID 控制器在第 \(k－1\) 个采样时刻的输出控制值 \(u_{k-1}\) 等于：

\[ u_{k-1} = K_p \times \Biggl[ e_{k-1} + \frac{T}{T_i} \times \sum^{k-1}_{j=0} e_j + T_d \times \frac{(e_{k-1} - e_{k-2})}{T} \Biggl] \]

联立并且化简上述两组公式，就可以整理得到增量式 PID 控制算法的公式：

\[ \begin{align} \Delta u_k & = u_k - u_{k-1} \\ & = K_p \Biggl(e_k - e_{k-1} + \frac{T}{T_i}e_k + T_d \frac{e_k - 2e_{k-1} + e_{k-2}}{T} \Biggl) \\ & = K_p \Biggl(1 + \frac{T}{T_i} + \frac{T_d}{T} \Biggl) e_k - K_p \Biggl( 1 + \frac{2T_d}{T} \Biggl) e_{k-1} + \Biggl( K_p \frac{T_d}{T} e_{k-2} \Biggl) \end{align} \]

如果使用参数 A 来替代上面公式当中的 \(K_p \times \Big(1 + \frac{T}{T_i} + \frac{T_d}{T} \Big)\) 部分，参数 B 替代上面公式当中的 \(K_p \times \Big( 1 + \frac{2T_d}{T} \Big)\) 部分，参数 C 替代上面公式当中的 \(K_p \times \frac{T_d}{T}\) 部分，就可以将增量式 PID 控制算法的公式简化为下面的形式：

\[ \begin{cases} A = K_p \times \Big(1 + \frac{T}{T_i} + \frac{T_d}{T} \Big) \\ B = K_p \times \Big( 1 + \frac{2T_d}{T} \Big) \\ C = K_p \times \frac{T_d}{T} \end{cases} \implies \Delta u_k = A_{e_k} - B_{e_{k-1}} + C_{e_{k-2}} \]

观察上述推导过程，如果 PID 控制系统采用恒定的采样周期 T，一旦确定 A、B、C 的参数值，仅仅只需要基于前后三次的测量偏差，就可以由上面的公式求解得到控制量 \(u_k\)。增量式 PID 控制算法相比于位置式 PID 算法的运算量更少，因而实际应用更加广泛。而位置式 PID 控制算法也可以通过增量式控制算法，推导得到如下的数字递推 PID 控制算法的公式：

\[ u_k = u_{k-1} + \Delta u_k \]

PID 算法的 C 程序实现

本节内容会将前面所述的繁杂 PID 数学推导，抽象为 C 语言编写的板级支持包（BSP，Board Support Package）程序，该程序主要由 BSP_PID.h 头文件和 BSP_PID.c 源文件组成，以便于大家在实际工程当中参考移植。

位置式 PID 的代码实现

对于位置式 PID 算法的程序实现，需要在头文件 BSP_PID.h 当中定义一个名称为 _PID 的结构体变量，并且同时声明 PID_param_init() 与 PID_Realize() 两个工具函数：

#ifndef __BSP_PID_H
#define __BSP_PID_H

typedef struct {
  float target_value;   // 目标值
  float actual_value;   // 实际值

  float err;            // 偏差值
  float err_last;       // 前一个偏差值

  float Kp, Ki, Kd;     // 定义比例、积分、微分系数

  float integral;       // 定义积分值
} _PID;

extern void PID_Parameter_Init(void);             // PID 参数初始化
extern float PID_Realize(float temporary_value);  // PID 算法具体实现

#endif

源文件 BSP_PID.c 当中定义的 PID_Parameter_Init() 函数主要用于配置 PID 算法所涉及到的 \(K_p\)、\(K_i\)、\(K_d\) 等各类结构体成员参数的值：

#include "./BSP_PID.h"

_PID PID; // 定义全局结构体变量

/** @brief 初始化 PID 参数 */
void PID_Parameter_Init() {
  PID.target_value = 0.0;
  PID.actual_value = 0.0;

  PID.err = 0.0;
  PID.err_last = 0.0;

  PID.integral = 0.0;

  PID.Kp = 0.31;
  PID.Ki = 0.070;
  PID.Kd = 0.3;
}

源文件 BSP_PID.c 当中定义的 PID_Realize() 函数是整个工程的核心，通过函数参数 temporary_value 将实际值传入，目标值通过代码当中的 PID.err = PID.target_value - PID.actual_value 参与计算，然后返回一个经过 PID 计算之后的实际值 actual_value，整个过程紧密围绕着前面定义的 _PID 结构体类型来进行：

/**
 * @brief  实现 PID 算法
 * @param  temporary_value 目标值
 * @retval 经过 PID 算法处理之后的输出值
 */
float PID_Realize(float temporary_value) {
  PID.target_value = temporary_value;            // 传入目标值
  PID.err = PID.target_value - PID.actual_value; // 计算目标值与实际值的偏差
  PID.integral += PID.err;                       // 累积偏差值

  /* PID 算法的具体实现 */
  PID.actual_value = PID.Kp * PID.err + PID.Ki * PID.integral + PID.Kd * (PID.err - PID.err_last);

  PID.err_last = PID.err;   // 传递偏差值
  return PID.actual_value;  // 返回实际值
}

上面代码当中的 PID 算法具体实现，就是基于前面所述的 PID 离散表达公式来进行实现的。不同之处在于下面公式中的第 2 项 \(K_i\) 使用的是对偏差进行积分，而在 C 程序代码当中变为对偏差进行累加。虽然表达形式上有所不同，但是内涵和作用是基本相同的：

\[ u(k) = K_p err(k) + K_i \sum err(k) + K_d \Big( err(k) - err(k-1) \Big) \]

把函数 PID_Realize() 放置到定时器中断里进行调用，定时器每间隔 20ms 中断一次，相应的 PID 算法也就会每 20ms 被执行一次（这就是 PID 算法的执行周期）。通过微控制器运行之后，将 PID_Realize() 输出的结果（也就是实际值 actual_value）打印到串口，从而得到如下的图像：

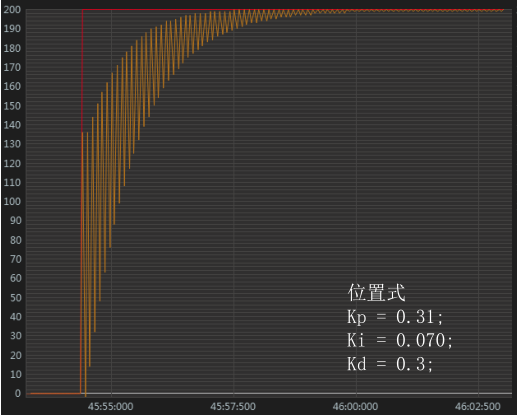
观察上面的数据，可以发现起初相邻两个数据差距较大，振荡较为严重。但是随着算法的持续运行，目标值与实际值之间的偏差变小，直到最后实际值会在目标值附近上下振动，这种微小的振动就是静态偏差。

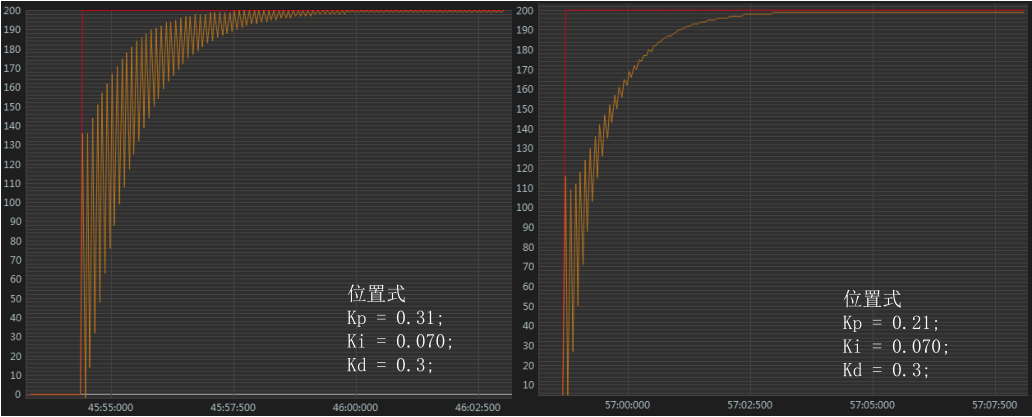
接着修改参数 \(K_p\) 并观察曲线的变化，上图左侧是 \(K_p = 0.31\) 时候输出的曲线，明显是在震荡了许多次之后才逐渐趋于稳定。而右侧是 \(K_p = 0.21\) 时候输出的曲线，调节次数和振荡明显减少，由此可见 PID 参数标定的重要性。

增量式 PID 的代码实现

实现增量式 PID 算法，头文件 BSP_PID.h 中依然需要定义一个名为 _PID 的结构体（相比于位置式 PID 里的结构体，这里增加了一个 err_next 成员变量，移除了一个表示积分值的 integral 成员变量），并且同样声明有 PID_param_init() 和 PID_Realize() 两个工具函数：

#ifndef __BSP_PID_H
#define __BSP_PID_H

typedef struct {
  float target_value;   // 目标值
  float actual_value;   // 实际值

  float err;            // 当前偏差值
  float err_next;       // 下一个偏差值
  float err_last;       // 最后一个偏差值

  float Kp, Ki, Kd;     // 比例、积分、微分系数
} _PID;

extern void PID_Parameter_Init(void);             // PID 参数初始化
extern float PID_Realize(float temporary_value);  // PID 算法具体实现

#endif

源文件 BSP_PID.c 当中定义的 PID_Parameter_Init() 函数，同样用于设定 PID 算法所涉及到的 \(K_p\)、\(K_i\)、\(K_d\) 以及 \(err\)、\(err_{last}\)、\(err_{next}\) 等结构体成员参数：

#include "./BSP_PID.h"

_PID PID; // 定义全局结构体变量

/** @brief 初始化 PID 参数 */
void PID_Parameter_Init() {
  PID.target_value = 0.0;
  PID.actual_value = 0.0;

  PID.err = 0.0;
  PID.err_last = 0.0;
  PID.err_next = 0.0;

  PID.Kp = 0.20;
  PID.Ki = 0.80;
  PID.Kd = 0.01;
}

源文件 BSP_PID.c 当中定义的 PID_Realize() 函数也同样是整个工程的核心，依然是通过参数 temporary_value 将实际值传入，然后经过一系列 PID 的计算处理之后，返回得到的实际值 actual_value，区别主要在于代码当中 PID 算法的具体实现部分：

/**
 * @brief  实现 PID 算法
 * @param  temporary_value 目标值
 * @retval 经过 PID 算法处理之后的输出值
 */
float PID_Realize(float temporary_value) {
  PID.target_value = temporary_value;             // 传入目标值
  PID.err = PID.target_value - PID.actual_value;  // 计算目标值与实际值的偏差

  /* PID 算法的具体实现 */
  float increment_value = PID.Kp * (PID.err - PID.err_next) + PID.Ki * PID.err + PID.Kd * (PID.err - 2 * PID.err_next + PID.err_last);
  PID.actual_value += increment_value;  // 对 PID 算法的处理结果进行累加处理

  PID.err_last = PID.err_next;          // 将下一个偏差，赋值给最后一个偏差
  PID.err_next = PID.err;               // 将当前偏差，赋值给下一个偏差

  return PID.actual_value;              // 返回实际值
}

上面代码当中的 PID 算法具体实现，就是基于前面所述的增量式 PID 算法的两个公式来进行实现的，程序代码的处理步骤（即代码中对于 increment_value 和 actual_value 变量值的处理过程）与 PID 算法公式基本保持一致。仔细观察可以发现，增量式 PID 算法总是与最近三次的偏差值相关：

\[ \begin{cases} \Delta u(k) = \Bigg( K_p \times \Big( err(k) - err(k - 1) \Big) \Bigg) + \Bigg( K_i \times \Big( err(k) \Big) \Bigg) + \Bigg( K_d \times \Big(err(k) - 2 \times err(k-1) + err(k-2) \Big) \Bigg) \\ u(k) = u(k-1) + \Delta u(k) \end{cases} \]

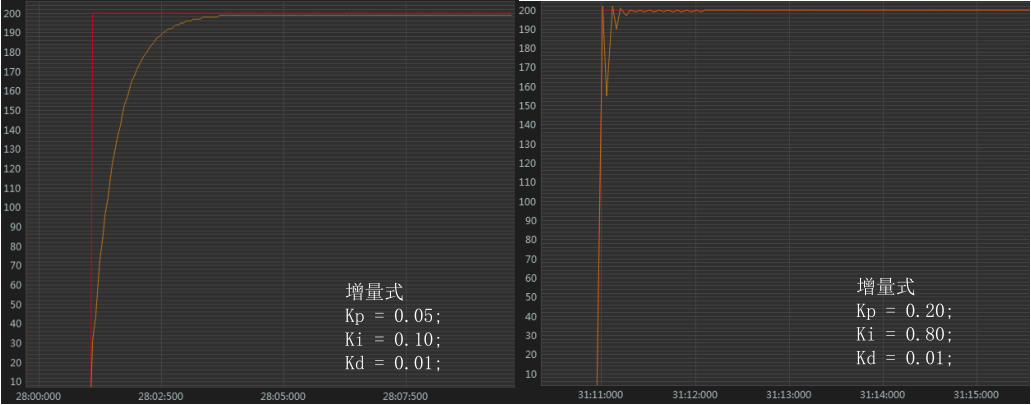
下图分别展示了 PID 系数分别等于 \(K_p=0.05\)、\(K_i=0.10\)、\(K_d=0.01\)（下图左），以及分别为 \(K_p=0.20\)、\(K_i=0.80\)、\(K_d=0.01\)（下图右）时候的输出曲线，可以看到不同的 PID 参数标定对于输出结果的影响：

控制参数的标定

在本文前面的内容当中，已经再三强调过 PID 控制参数的标定，对于控制输出结果的重要性。虽然可以通过理想化的数学模型，计算出 PID 控制相关的参数，但是这种方法并不总是能完美的匹配实际工况，还需要结合一些工程化的标定方法进行调参，这些方法包括 试凑法、临界比例法、一般调节法 等。

首先，我们总结一下 PID 算法各个控制系数的调节作用，以便于在后续的 PID 参数标定当中做到有的放矢：

1. 比例系数：调节作用快，PID 控制系统一旦出现偏差，就会立刻对偏差进行放大输出。
2. 积分系数：用于调节 输入偏差值 对于 输出控制信号 的影响程度，如果积分系数标定得越大，那么 PID 控制系统消除静态偏差的时间就会越短（但是过大的积分系数又会导致超调现象的发生）。
3. 微分系数：用于调节偏差变化量对于控制系统输出的影响程度，如果微分系数标定得越大，那么 PID 控制系统对于偏差量的变化就会越敏感，也就越能提前进行响应，从而抑制超调现象，但是过大的微分系数又会导致振荡现象的出现。

试凑法

基于当前控制系统的具体情况，首先试凑出几组经验值，然后观察系统输出曲线的变化规律，大致确定各个系数对于曲线的具体影响，最后再根据具体的曲线进行调整。试凑法需要遵循首先调节 比例系数，然后调节 积分系数，最后调节 微分系数 的顺序，大致上遵循如下的标定过程：

1. 按照纯比例控制系统来标定 比例系数，得到一个比较理想的控制信号输出曲线。
2. 把比例系数缩小 1.2 倍左右，再将 积分系数 从小到大进行调整，使其输出一个满意的控制信号输出曲线。
3. 基于上面的 积分系数 重新标定 比例系数，观察输出的控制信号曲线是否有所改善。
4. 如果存在改善，就再次修改 积分系数，如此多次反复，直至得到一组合适的 比例系数 和 积分系数。
5. 如果外界存在干扰信号，控制系统的稳定性不佳，可以适当缩小 比例系数 和 积分系数，确保控制系统的稳定工作。
6. 如果控制系统存在小幅超调，则可以在缩小 比例系数 和 积分系数 的同时，适当的增大 微分系数，从而获得超调量最小，调节作用时间最短的控制信号输出曲线。

临界比例法

基于纯比例控制系统，按照从小到大的顺序逐渐调节 比例系数，直至控制系统输出信号曲线出现等幅振荡，再根据经验公式计算参数。该方法大体上遵循如下的标定过程：

1. 将 积分系数、微分系数 置零，调节 比例系数 选取一个适当的值，使得控制系统按照纯比例的方式运行。
2. 逐步增大比例系数，观察控制信号输出曲线的变化。如果曲线波动衰减，则继续增大比例系数。如果曲线波动发散，则减小比例系数，直至曲线波动呈现出等幅振荡，此时记录下这个临界的比例系数 \(\delta K\) 和振荡周期 \(T_k\) 的值。
3. 根据前面记录下的比例系数 \(\delta K\) 和振荡周期 \(T_k\) 值，采用如下表格当中的经验公式，就可以计算出 \(K_p\)、\(K_i\)、\(K_d\) 的参数。

控制环节	比例系数 \(K_p\)	积分系数 \(K_i\)	微分系数 \(K_d\)
P	\(\frac{\delta K}{2}\)	\(0\)	\(0\)
PI	\(\frac{\delta K}{2.2}\)	\(\frac{K_p}{0.833 \times T_k}\)	\(0\)
PID	\(\frac{\delta K}{1.7}\)	\(\frac{K_p}{0.5 \times T_k}\)	\(0.125 \times T_k \cdot K_p\)

通用调节法

这种方法主要针对于一些通用的 PID 控制系统，具体的标定调试过程如下面列表所示：

1. 首先，将积分系数与微分系数置零，简化控制系统为纯比例控制。
2. 把比例系数的值设定为控制系统允许最大值的 60% ~ 70%，逐步增大比例系数直至出现振荡，再逐渐减小比例系数直至消除振荡。
3. 记录下此时的比例系数，并且再次将控制系统的比例系数设定为当前值的 60% ~ 70%。
4. 确定好比例系数后，设定一个较小的积分系数，然后逐渐增大该积分系数，同样直至出现振荡，再逐渐减小积分系数直至消除振荡。
5. 记录下此时的积分系数，并且将控制系统的积分系数标定为当前值的 55% ~ 65%。
6. 通常情况下，不需要设置微分系数（标定为 0 即可），如果出现小幅振荡，并且通过比例和积分环节无法消除，那么就可以考虑采纳与上述比例系数和积分系数标定类似的方法，此时微分系数可以取控制系统不发生振荡时值的 30% 左右。
7. 基于上述步骤获取的参数进行标定，分别对控制系统进行空载和带载的调试，然后再进行相应的微调，直至满足目标需求。

PID 参数标定实例

本节内容会基于一个实际的 PID 控制系统输出曲线，展示 PID 各个系数的调节效果。首先，调整比例系数（积分系数和微分系数全部设置为零），此时控制系统只有比例环节参与控制，如果控制系统的输出曲线出现下图所示的大幅振荡。需要先排除硬件上的故障（例如电压不稳、电机堵转等），排除硬件因素的影响之后，说明当前的比例系数可能标定得过大，需要可以适当减小比例系数，同时观察曲线的变化，直至曲线的大幅度振荡消失。

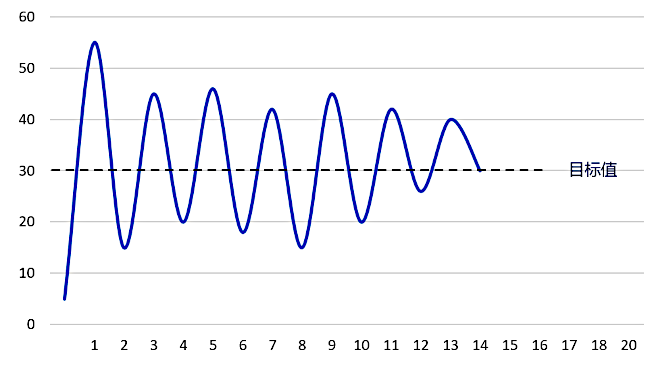
若输出曲线依旧存在有如下图所示的小幅超调，并且无法再通过比例系数来优化曲线。此时可以逐步增大微分系数，同时观察输出曲线的变化，进而找出比较合适的参数。增大微分系数之后，如果输出曲线趋近于理想，则说明该控制系统只需要保留 比例环节 和 微分环节 的控制。

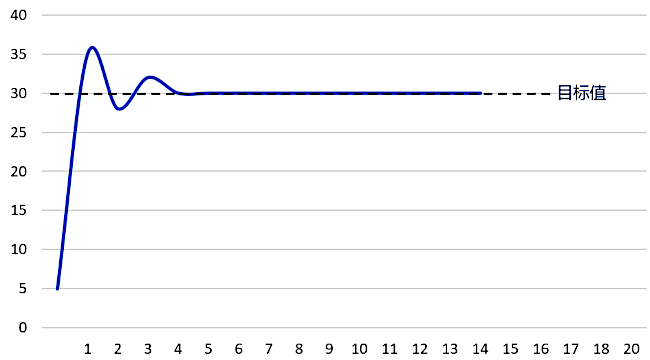
如果此时控制系统的实际输出值，依然无法达到目标值，始终存在有下图所示的静态误差。那么就可以改为逐步增大积分系数，并且同时观察输出曲线的变化，如果消除静态误差的时间过长，则可以继续增大积分系数（注意控制系统的超调幅度）。经过调整之后，如果输出曲线趋于理想，则说明该控制系统仅需要保留 比例环节 和 积分环节 的控制：

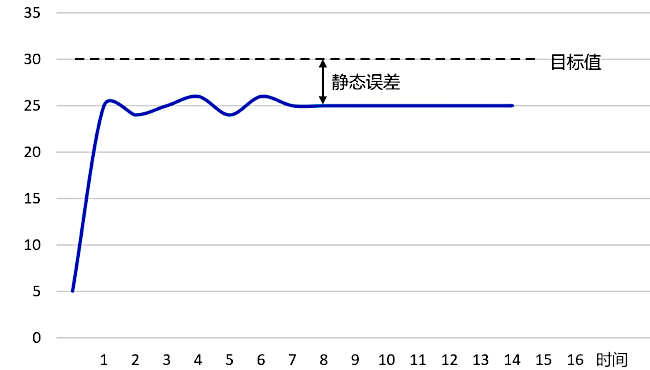
如果此时依然存在小幅的超调现象，那么就可以逐步增大微分系数，同时观察输出曲线的变化，进而找出最为合适的参数。实际生产环境下，自动化控制系统纷繁复杂，上面展示的标定过程仅仅只能作为参考。实际的日常工作当中，建议选择一款 PID 调试上位机软件，借助直观的图形化输出，便于调试出更加合理的参数标定。