高等数学主要概念与公式摘要
高等数学是由微积分学,较为深入的代数学、几何学以及它们之间的交叉内容所形成的一门基础学科。由于电路分析、运算放大器、信号完整性、高频电路和信号学当中,都涉及有大量的积分和导数运算,也需要经常使用到拉普拉斯和傅立叶变换等高等数学内容,因此着手撰写本文用于复习大学本科学习阶段涉及的微积分知识,主要包含一元函数微分学、一元函数积分学、矢量代数与空间解析几何、多元函数微分学、多元函数积分学、无穷级数、常微分方程等部分的内容。

由于微积分涉及的概念相对较为抽象,因此在文章写作过程中,阅读并且参考了《Thomas’ Calculus》一书当中的有关内容。该书从 1951 年第 1 版发行至今,当前的最新版本为第 14 版,已经足足经历了七十个年头,是一本经历过时间检验的优秀参考资料。对于本文当中所涉及到的代数学知识,可以参见博主撰写的另外一篇数学类文章《初等代数常用公式与图像汇总》。
函数与极限
数列的极限
数列极限的定义
➤ 如果按照某一个法则,对于每一个 \(n \in N\),都对应着一个确定的实数 \(x_n\),这些实数 \(x_n\) 按照下标 \(n\) 从小到大排列得到的一个序列 \(x_1, x_2, x_3, ... , x_n, ...\) 就叫做数列,简记为 \(\{ x_n \}\)。数列当中的每一个数叫做数列的项,其中的第 \(n\) 项叫做数列的一般项或者通项。
几何上,可以将数列 \(\{ x_n \}\) 视为数轴上的一个动点,它依次取数轴上的点 \(x_1,x_2,x_3,...,x_n,...\):
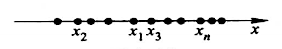
注意:数列 \(\{ x_n \}\) 可以视为自变量为正整数 \(n\) 的函数 \(x_n = f(n),\ n \in N_+\),当自变量 \(n\) 依次取
1,2,3...等一切正整数时,对应的函数值就组成了一个数列 \(\{ x_n \}\)。
➤ 假设 \(\{x_n\}\) 为一个数列,如果存在常数 \(a\),对于任意给定的正数 \(\varepsilon\) (无论它多么小),总存在正整数 \(N\),使得当 \(n>N\) 时,不等式 \(\vert x_n - a \vert < \varepsilon\) 都成立,那么就称常数 \(a\) 是数列 \(\{ x_n \}\) 的极限,或者称数列 \(\{x_n\}\) 收敛于 \(a\),记为:
\[ \lim\limits_{n \to \infty} x_n = a \ 或者 \ x_n \to a (n \to \infty) \]
如果不存在这样的常数 \(a\),就说明数列 \(\{x_n\}\) 没有极限,或者说数列 \(\{x_n\}\) 是发散的,习惯上也就是说 \(\lim\limits_{n \to \infty} x_n\) 不存在。
注意:上面定义当中的正数 \(\varepsilon\) 可以任意给定非常重要,因为只有满足了这个前提条件,不等式 \(|x_n - a|<\varepsilon\) 才能够表达出 \(x_n\) 与 \(a\) 无限接近的意思,除此之外,还需要注意定义当中的正整数 \(N\) 是与任意给定的正数 \(\varepsilon\) 相关的,它会随着 \(\varepsilon\) 的给定而选定。
几何上,数列 \(\{ x_n \}\) 的极限为 \(a\) 是将常数 \(a\) 以及数列 \(x_1,x_2,x_3,...,x_n,...\),在数轴上用其对应的点表示出来,再在数轴上作点 \(a\) 的邻域,即开区间 \((a - \varepsilon, a + \varepsilon)\):

注意:由于不等式 \(|x_n - a| < \varepsilon\) 与不等式 \(a - \varepsilon < x_n < a + \varepsilon\) 等价,所以当 \(n > N\) 时,所有的点 \(x_n\) 都位于开区间 \((a - \varepsilon, a + \varepsilon)\) 之内,而只存在有限个(最多只有 \(N\) 个)处于区间之外。
➤ 用符号 \(\forall\) 表示对于每一个,符号 \(\exists\) 表示存在,那么数列极限 \(\lim\limits_{n \to \infty} x_n\) 的定义可以表达为:
\[ \lim\limits_{n \to \infty} x_n \iff \forall \varepsilon > 0,\exists 正整数 N,当 n > N 时,有 \vert x_n - a \vert < \varepsilon \]
收敛数列的性质
➤ 下面的四个定理,都是有关于收敛数列的性质:
- 定理 1:极限的唯一性,如果数列 \(\{ x_n \}\) 收敛,那么它的极限唯一;
- 定理 2:收敛数列的有界性,如果数列 \(\{ x_n \}\) 收敛,那么数列 \(\{ x_n \}\) 一定有界;
- 定理 3:收敛数列与其子数列间的关系,如果数列 \(\{ x_n \}\) 收敛于 \(a\),那么它的任意一个子数列也收敛,并且极限也是 \(a\);
- 定理 4:收敛数列的保号性,如果 \(\lim\limits_{n \to \infty} x_n = a\),且 \(a > 0\) (或者 \(a < 0\)),那么存在正整数 \(N\),当 \(n > N\) 时,都有 \(x_n > 0\) (或者 \(x_n < 0\));
推论:如果数列 \(\{ x_n \}\) 从某项起有 \(x \ge 0\) (或者 \(x \le 0\)),并且 \(\lim\limits_{n \to \infty} x_n = a\),那么 \(a \ge 0\) (或者 \(a \le 0\));
子数列
➤ 任意抽取数列 \(\{ x_n \}\) 里的无限多项,并且保持这些项在原数列当中的先后次序,这样得到的数列就称为原数列的子数列或子列。
假设在数列 \(\{ x_n \}\) 当中,第一次抽取 \(\{ x_{n_1} \}\),第二次抽取 \(\{ x_{n_1} \}\) 后面的 \(\{ x_{n_2} \}\),第三次抽取 \(\{ x_{n_2} \}\) 后面的 \(\{ x_{n_3} \}\),如此循环往复,就可以得到如下的数列:
\[ \{ x_{n_1}, x_{n_2}, x_{n_3} ..., x_{n_k}, ... \} \]
这里的数列 \(\{ x_{n_k}
\}\) 就是数列 \(\{ x_n
\}\) 的子数列。其中的一般项
\(x_{n_k}\)
是指子数列的第 k
项,原数列的第 n 项。
函数的极限
函数极限的一般概念
➤ 函数极限的一般概念:如果在自变量的某个变化过程当中,对应的函数值无限接近于某个确定的数,那么这个确定的数就称为该变化过程当中的函数极限。这个极限与自变量的变化过程密切相关,自变量的变化过程不同,函数极限的表现形式就会不同:
- 自变量 \(x\) 任意的趋近于有限值 \(x_0\) 时(记作 \(x \to x_0\)),对应的函数值 \(f(x)\) 的变化情况;
- 自变量 \(x\) 的绝对值 \(|x|\) 趋近于无穷大 \(\infty\) 时(记作 \(x \to \infty\)),对应的函数值 \(f(x)\) 的变化情况;
自变量趋于有限值
➤
自变量趋于有限值时函数的极限:假设函数
\(f(x)\) 在点 \(x_0\)
的某一个去心邻域内有定义,如果存在常数
A,对于任意给定的正数 \(\varepsilon\)
(不论多么小),总存在着正数 \(\delta\),使得当 \(x\) 满足不等式 \(0 < |x - x_0| < \delta\)
时,对应的函数值 \(f(x)\) 都满足不等式 \(|f(x) - A| <
\varepsilon\),那么常数 A
就称为函数 \(f(x)\) 当
\(x \to x_0\)
时候的极限,记作:
\[ \lim\limits_{x \to x_0} f(x) = A\ 或者\ f(x) \to A\ (当 x \to x_0) \]
这个定义可以简单的表述为如下形式:
\[ \lim\limits_{x \to x_0} f(x) = A \iff \forall \varepsilon > 0,\ \exists\ \delta > 0,\ 当 0<|x - x_0|< \delta 时,\ 有 |f(x) - A| < \varepsilon \]
注意:上述定义里的 \(0 < |x - x_0|\) 表示的是 \(x \neq x_0\),所以 \(x \to x_0\) 时函数 \(f(x)\) 有无极限,与函数 \(f(x)\) 在点 \(x_0\) 是否有定义并无关联。
➤ 函数 \(f(x)\) 当 \(x \to x_0\) 时的极限为 A
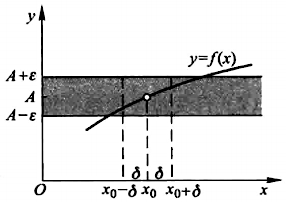
的几何解释:对于任意给定的一个正数 \(\varepsilon\) 作平行于 \(x\) 轴的两条直线 \(y = A + \varepsilon\) 以及 \(y = A -
\varepsilon\),介于两条直线之间的是一个横条区域。根据定义,对于给定的
\(\varepsilon\),存在着点
\(x_0\) 的一个 \(\delta\) 邻域 \((x_0 - \delta, x_0 + \delta)\),当 \(y = f(x)\)
图形上的点的横坐标 \(x\) 在邻域 \((x_0 - \delta, x_0 + \delta)\) 内,但是
\(x \neq x_0\)
时,这些点的纵坐标 \(f(x)\) 满足不等式 \(|f(x) - A| < \varepsilon\) 或者 \(A - \varepsilon < f(x) < A +
\varepsilon\),即这些点都位于下图当中的横条区域:
➤ 在 \(\lim\limits_{x \to x_0} f(x) =
A\) 的定义当中,将 \(0 < |x - x_0|
< \delta\) 更改为 \(x_0 - \delta
< x < x_0\),那么 A
就称为函数 \(f(x)\) 当
\(x \to x_0\)
时的左极限,记作:
\[ \lim\limits_{x \to x_{0}^{-}} f(x) = A 或者 f(x_{0}^{-}) = A \]
➤ 类似的,在 \(\lim\limits_{x \to x_0} f(x)
= A\) 的定义当中,将 \(0 < |x - x_0|
< \delta\) 更改为 \(x_0 < x <
x_0 + \delta\),那么 A 就称为函数
\(f(x)\) 当 \(x \to x_0\)
时的右极限,记作:
\[ \lim\limits_{x \to x_{0}^{+}} f(x) = A 或者 f(x_{0}^{+}) = A \]
➤ 左极限与右极限统称为单侧极限,根据 \(x \to x_0\) 时函数 \(f(x)\) 极限的定义,以及左极限与右极限的定义,可以容易的证明:函数 \(f(x)\) 当 \(x \to x_0\) 时极限存在的充分必要条件是左极限、右极限各自存在并且相等,即
\[ f(x_0^{-}) = f(x_0^{+}) \]
注意:即使 \(f(x_0^{-})\) 和 \(f(x_0^{+})\) 都存在,但是两者如果不相等,则 \(\lim\limits_{x \to x_0} f(x)\) 也不会存在。
自变量趋于无穷大
➤
自变量趋于无穷大时函数的极限:假设函数
\(f(x)\) 当 \(|x|\)
大于某一个正数时有定义,如果存在常数
A,对于任意给定的正数 \(\varepsilon\)
(无论多么小),总存在着正数 X,使得当 \(x\) 满足不等式 \(|x| > X\)
时,对应的函数值都满足不等式 \(|f(x) - A| <
\varepsilon\),那么常数 A
就称为函数 \(f(x)\) 当
\(x \to \infty\)
时候的极限,记作:
\[ \lim\limits_{x \to \infty} f(x) = A\ 或者\ f(x) \to A\ (当 x \to \infty) \]
这个定义同样可以简单的表述为如下形式:
\[ \lim\limits_{x \to \infty} f(x) = A \iff \forall \varepsilon > 0,\ \exists\ X > 0,\ 当 |x| > X 时,\ 有 |f(x) - A| < \varepsilon \]
- 如果 \(x > 0\) 并且无限增大 (记作 \(x \to +\infty\)),那么只要将上述定义中的 \(|x| > X\) 更改为 \(x > X\),就可以得到 \(\lim\limits_{x \to +\infty} f(x) = A\) 的定义。
- 如果 \(x < 0\) 并且 \(|x|\) 无限增大 (记作 \(x \to -\infty\)),那么只要将上述定义中的 \(|x| > X\) 更改为 \(x < -X\),就可以得到 \(\lim\limits_{x \to -\infty} f(x) = A\) 的定义。
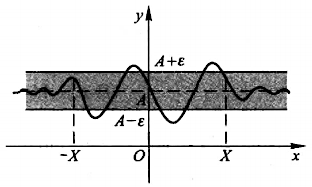
➤ \(\lim\limits_{x \to \infty} f(x)
= A\) 的几何意义:作直线 \(y = A - \varepsilon\) 和 \(y = A +
\varepsilon\),则总有一个正数 X
存在,使得当 \(x > X\) 或者 \(x < -X\) 时,函数 \(y = f(x)\)
的图形位于这两条直线之间,此时直线 \(y = A\) 就是函数 \(y = f(x)\)
的图形的水平渐近线。
函数极限的性质
➤ 这里以 \(\lim\limits_{x \to x_0} f(x)\) 形式为代表,给出关于函数极限性质的一些定理:
- 定理 1:函数极限的唯一性,如果 \(\lim\limits_{x \to x_0} f(x)\) 存在,那么该极限唯一;
- 定理 2:函数极限的局部有界性,如果 \(\lim\limits_{x \to x_0} f(x) = A\),那么存在常数 \(M > 0\) 和 \(\delta > 0\),使得当 \(0 < |x - x_0| < \delta\) 时,有 \(|f(x)| \leq M\);
- 定理 3:函数极限的局部保号性,如果 \(\lim\limits_{x \to x_0} f(x) = A\),并且 \(A > 0\) (或者 \(A < 0\)),那么存在常数 \(\delta > 0\),使得当 \(0 < |x - x_0| < \delta\) 时,有 \(f(x) > 0\) (或者 \(f(x) < 0\));
- 定理 3':基于定理 3 可以进一步得出结论,如果 \(\lim\limits_{x \to x_0} f(x) = A\ (A \neq 0)\),那么就存在着的某一个去心邻域 \(\overset{o}{U}(x_0)\),当 \(x \in \overset{o}{U}(x_0)\) 时,就有 \(|f(x)| > \frac{|A|}{2}\);
推论:如果在 \(x_0\) 的某一个去心邻域内 \(f(x) \ge 0\) (或者 \(f(x) \le 0\)),并且 \(\lim\limits_{x \to x_0} f(x) = A\),那么 \(A \ge 0\) (或者 \(A \le 0\))。
- 定理 4:函数极限与数列极限的关系,如果极限 \(\lim\limits_{x \to x_0} f(x)\) 存在,\(\{x_n \}\) 为函数 \(f(x)\) 的定义域内任一收敛于 \(x_0\) 的数列,并且满足 \(x_n \neq x_0\ (n \in N_+)\),那么相应的函数值数列 \(\{ f(x_n) \}\) 必然收敛,并且 \(\lim\limits_{n \to \infty} f(x_n) = \lim\limits_{x \to x_0} f(x)\);
无穷大 & 无穷小
➤ 无穷小的定义:如果函数 \(f(x)\) 当 \(x \to x_0\) (或者 \(x \to \infty\))时的极限为零,那么就称函数 \(f(x)\) 为当 \(x \to x_0\) (或者 \(x \to \infty\))时的无穷小。
➤ 无穷小与函数极限的关系:在自变量的同一个变化过程 \(x \to x_0\) (或者 \(x \to \infty\))当中,函数 \(f(x)\) 具有极限 \(A\) 的充分必要条件是 \(f(x) = A + \alpha\),其中 \(\alpha\) 是无穷小。
➤ 无穷大的定义:假设函数 \(f(x)\) 在 \(x_0\) 的某一个去心邻域内有定义 (或者 \(|x|\) 大于某一个正数时有定义),如果对于任意给定的正数 \(M\) (无论它多么大),总存在着正数 \(\delta\) (或者正数 \(X\)),只要 \(x\) 适合不等式 \(0 < |x - x_0| < \delta\) (或者 \(|x| > X\)),对应的函数值 \(f(X)\) 总是满足不等式 \(|f(x)| > M\),那么就称函数 \(f(x)\) 是当 \(x \to x_0\) (或者 \(x \to \infty\)) 时的无穷大。
➤ 函数的极限为无穷大:根据函数极限的定义,当 \(x \to x_0\) (或者 \(x \to \infty\)) 时,无穷大的函数 \(f(x)\) 极限不存在,但是为了便于叙述函数的这一状态,也可以表述成函数的极限为无穷大,并且记为:
\[ \lim\limits_{x \to x_0} f(x) = \infty\ (或者 \lim\limits_{x \to \infty} = \infty) \]
如果将无穷大定义当中的 \(|f(x)| > M\) 更换为 \(f(x) > M\) (或者 \(f(x) < -M\)),那么就可以记作:
\[ \lim\limits_{\begin{aligned} &x \to x_0 \\ (&x \to \infty) \end{aligned}} f(x) = + \infty \ (或者 \lim\limits_{\begin{aligned} &x \to x_0 \\ (&x \to \infty) \end{aligned}} f(x) = - \infty) \]
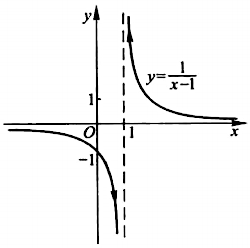
一般而言,如果 \(\lim\limits_{x \to x_0} f(x)= \infty\),那么直线 \(x = x_0\) 就是函数 \(y = f(x)\) 的图形的铅直渐近线。例如对于 \(\lim\limits_{x \to 1} \frac{1}{x - 1} = \infty\) 而言,直线 \(x = 1\) 就是函数 \(y = \frac{1}{x - 1}\) 图形上面的一条铅直渐近线:
➤ 无穷大与无穷小之间的关系:在自变量的同一个变化过程当中,如果 \(f(x)\) 为无穷大,那么 \(\frac{1}{f(x)}\) 为无穷小;反之,如果 \(f(x)\) 为无穷小,并且 \(f(x) \neq 0\),那么 \(\frac{1}{f(x)}\) 为无穷大。
高等数学主要概念与公式摘要