磁场定向控制（FOC，Field-Oriented Control）是一种用于无刷电机（BLDC）、永磁同步电机（PMSM）的矢量 控制算法，其核心思想是将电机定子的电流分解为两个正交的分量：一个用于产生磁场的励磁分量 d 轴和一个用于产生转矩的转矩分量 q 轴。通过对电机的 转矩 和 磁场 进行独立的控制，从而达到快速响应和精确控制的目的，并且降低运行时的噪音和振动。FOC 算法的处理过程可以大体划分为坐标变换、电流控制、逆变换、空间矢量调制（SVPWM）四个阶段。

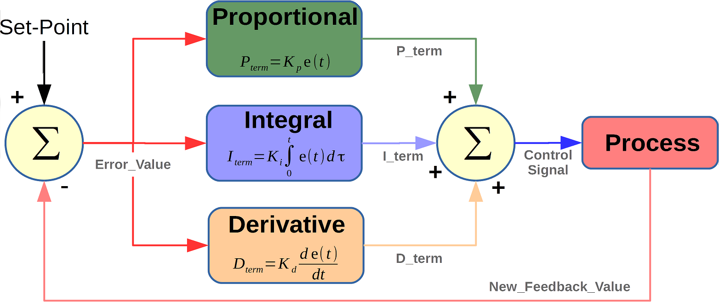
坐标变换阶段：将三相定子电流（\(I_a, I_b, I_c\)）通过 Clarke 变换转换为两相静止坐标系（\(I_\alpha, I_\beta\)），再通过 Park 变换将静止坐标系转换为旋转坐标系（\(I_d, I_q\)），其中 \(I_d\) 控制磁场，\(I_q\) 控制转矩。电流控制阶段，通过 PI 控制器调节 \(I_d\) 和 \(I_q\)，使其跟踪参考值。\(I_d\) 的参考值通常设置为零（对于永磁同步电机）或根据需要进行调节（对于感应电机）。\(I_q\) 的参考值由转矩需求决定。逆变换阶段，将旋转坐标系下的电压（\(V_d, V_q\)）通过逆 Park 变换转换回静止坐标系（\(V_\alpha, V_\beta\)），再通过逆 Clarke 变换生成三相电压信号，用于驱动逆变器。空间矢量调制阶段：将生成的电压信号调制为 PWM 信号，控制逆变器开关驱动电机。

比例-积分-微分（PID，Proportion Integration Differentiation）是一种广泛运用于自动化控制领域的经典算法，属于众多控制算法当中最能够体现反馈思想的算法。该算法由 Nicolas Minorsky 于 1922 年船舶舵机控制理论的研究当中提出，随后以其卓越的性能和易于实现的特性，在 温度控制、电机调速、过程控制 等诸多领域逐渐普及。无论是简单的单变量系统，还是复杂的多变量系统，PID 控制算法都能通过调节 比例、积分、微分 三个参数实现精准的控制。

例如把一台无刷电机连接到额定输出电压为 12V 的锂电池组，然后通过一个占空比为 50% 的 PWM 波进行驱动，刚开始的时候电机运行速度很快且扭矩充足，但是随着时间的流逝，锂电池的放电电压逐步下降，开始影响到电机的转速和转矩。如果这块锂电池组刚充满的时候，输出电压为 12V，PWM 波占空比为 50%，那么作用在电机两端的等效电压为 \(12V \times 50\% = 6V\)。放电持续一段时间之后，锂电池电压降低至 9V，此时电机两端的等效电压也会降低到 \(9V \times 50\% = 4.5V\)，电机的转速和转矩开始出现明显的下降。如果需要在锂电池的整个放电周期当中，保持电机 转速 和 转矩 的稳定，就有必要引入这里将要介绍的 PID 控制理论。